2022年7月的力扣每日一题...

【LeetCode】2022 7月 每日一题

前言

七月太忙了，又是项目又是练车又是各种比赛。大概有10天的每日一题没有当天写完（虽然后面补上了）。

将每日一题的所有思路记录在这里分享一下。

7.1 为运算表达式设计优先级

题目

241. 为运算表达式设计优先级

给你一个由数字和运算符组成的字符串 expression ，按不同优先级组合数字和运算符，计算并返回所有可能组合的结果。你可以 按任意顺序 返回答案。

生成的测试用例满足其对应输出值符合 32 位整数范围，不同结果的数量不超过 104 。

示例 1：

输入：expression = "2-1-1"
输出：[0,2]
解释：
((2-1)-1) = 0 
(2-(1-1)) = 2

示例 2：

输入：expression = "2*3-4*5"
输出：[-34,-14,-10,-10,10]
解释：
(2*(3-(4*5))) = -34 
((2*3)-(4*5)) = -14 
((2*(3-4))*5) = -10 
(2*((3-4)*5)) = -10 
(((2*3)-4)*5) = 10

提示：

• 1 <= expression.length <= 20
• expression 由数字和算符 '+'、'-' 和 '*' 组成。
• 输入表达式中的所有整数值在范围 [0, 99]

思路

本题是一道中等题，但是其思路万变不离其宗

复杂问题需要简单化，就需要分治。典型的分治问题

将一个表达式可以分成三个部分

• 左部分（当成一个计算出结果的数据）
• 中间部分（符号）
• 有部分（右边的计算出结果的数据）

这么分完之后，我们又可以对左部分进行分解成三部分，右部分分解成三部分

最后将所有的左部分和右部分得到的结果放入到数组中，返回这个数组即可

如果转化成代码，那么就可以使用dfs进行左中右的分治，dfs(left, right)表示在[left, right]区间所有的计算结果的可能，而这个可能又可以分解成[left, i-1]与[i, right]两部分的结果相并

代码

ts版本

function diffWaysToCompute(expression: string): number[] {
    const s: string = expression

    const calc: Function = (num1: number, num2: number, sign: string): number => {
        let res: number = 0
        switch(sign) {
            case '+':
            res = num1 + num2
            break
            case '-':
            res = num1 - num2
            break
            case '*':
            res = num1 * num2
        }
        return res
    }

    const dfs: Function = (left: number, right: number): number[] => {
        let res: number[] = []
        for (let i = left; i <= right; i++) {
            let c = s[i]
            if (c >= '0' && c <= '9') continue
            let lRes = dfs(left, i - 1)		// 左部分
            let rRes = dfs(i + 1, right)	// 右部分
            for (let lr of lRes) {
                for (let rr of rRes) {
                    res.push(calc(lr, rr, c))
                }
            }
        }
        // 计算数字
        if (res.length == 0) {
            let tmp = 0
            for (let i = left; i <= right; i++) {
                tmp = tmp * 10 + parseInt(s[i])
            }
            res.push(tmp)
        }
        return res
    }

    return dfs(0, s.length-1)
}

7.2 最低加油次数

题目

871. 最低加油次数

汽车从起点出发驶向目的地，该目的地位于出发位置东面 target 英里处。

沿途有加油站，每个 station[i] 代表一个加油站，它位于出发位置东面 station[i][0] 英里处，并且有 station[i][1] 升汽油。

假设汽车油箱的容量是无限的，其中最初有 startFuel 升燃料。它每行驶 1 英里就会用掉 1 升汽油。

当汽车到达加油站时，它可能停下来加油，将所有汽油从加油站转移到汽车中。

为了到达目的地，汽车所必要的最低加油次数是多少？如果无法到达目的地，则返回 -1 。

注意：如果汽车到达加油站时剩余燃料为 0，它仍然可以在那里加油。如果汽车到达目的地时剩余燃料为 0，仍然认为它已经到达目的地。

示例 1：

输入：target = 1, startFuel = 1, stations = []
输出：0
解释：我们可以在不加油的情况下到达目的地。

示例 2：

输入：target = 100, startFuel = 1, stations = [[10,100]]
输出：-1
解释：我们无法抵达目的地，甚至无法到达第一个加油站。

示例 3：

输入：target = 100, startFuel = 10, stations = [[10,60],[20,30],[30,30],[60,40]]
输出：2
解释：
我们出发时有 10 升燃料。
我们开车来到距起点 10 英里处的加油站，消耗 10 升燃料。将汽油从 0 升加到 60 升。
然后，我们从 10 英里处的加油站开到 60 英里处的加油站（消耗 50 升燃料），
并将汽油从 10 升加到 50 升。然后我们开车抵达目的地。
我们沿途在1两个加油站停靠，所以返回 2 。

提示：

1. 1 <= target, startFuel, stations[i][1] <= 10^9
2. 0 <= stations.length <= 500
3. 0 < stations[0][0] < stations[1][0] < ... < stations[stations.length-1][0] < target

思路

困难题。属于是思路想不到，但是一旦想到，直接可以开始写。

我们可以把这个题看作，每次经过加油站，直接把油抬走。每次到车没油了，再在所有抬上车的油箱中，选择油最多的邮箱进行加油（贪心）

这样如果车上的油可以让我们到目的地，就成功返回加油次数，否则就返回-1

既然我们要每次加油加最多油的油箱，有一个数据结构非常适合，那就是优先队列（堆），这里选择大根堆，每次最多油的油箱放在最上面，需要用的时候就把他拿出来

代码

ts没有自带的优先队列实现，我这里直接硬写了一个实现的非常垃圾的有序数组来模拟大根堆（实际上仅仅是模拟堆头是最大的这一个功能罢了，其他的结构完全对不上哈哈哈哈...），原理就是每次插入，大的数据就差在前面，就这么简单

function minRefuelStops(target: number, startFuel: number, stations: number[][]): number {
    let loc = 0 // 当前行驶的路程
    let res = 0 // 加油的次数
    let nowFuel = startFuel // 当前拥有的油量
    let heap = new Q()  // 可以加油的加油站油量存储
    let curIdx = 0  // 当前经过的加油站的idx
    let ssl = stations.length
    while (loc < target) {  // 只要没有到达target，就一直循环下去
        if (nowFuel == 0) { // 如果模拟到油没了，两种情况判断
            if (!heap.isEmpty()) {nowFuel += heap.poll(); res++}    // 大根堆里存在加油站可以加油
            else return -1  // 无法加油
        }
        loc += nowFuel
        nowFuel = 0 // 继续行驶剩余油量
        // 经过的加油站都存储到大根堆里
        while (curIdx < ssl && stations[curIdx][0] <= loc) {
            heap.push(stations[curIdx++][1])
            // console.log(heap.arr)
        }
    }
    return res
}

// 憨憨方式模拟大根堆
class Q {
    arr: number[]
    constructor() {
        this.arr = []
    }
    push(val: number) {
        if (this.arr.length == 0) {
            this.arr.push(val)
        } else {
            let l = this.arr.length
            for (let i = 0; i < l; i++) {
                let curItem = this.arr[i]
                if (val >= curItem) {
                    if (i == 0) {
                        this.arr = [val].concat(this.arr)
                    } else {
                        this.arr.splice(i, 0, val)
                    }
                    break
                } else if(val < curItem && i == l - 1) {
                    this.arr = this.arr.concat([val])
                }
            }
        }
    }
    poll() {
        return this.arr.shift() || 0
    }
    isEmpty() {
        return this.arr.length == 0
    }
}

7.3 下一个更大元素 III

题目

556. 下一个更大元素 III

给你一个正整数 n ，请你找出符合条件的最小整数，其由重新排列 n 中存在的每位数字组成，并且其值大于 n 。如果不存在这样的正整数，则返回 -1 。

注意 ，返回的整数应当是一个 32 位整数 ，如果存在满足题意的答案，但不是 32 位整数 ，同样返回 -1 。

示例 1：

输入：n = 12
输出：21

示例 2：

输入：n = 21
输出：-1

提示：

• 1 <= n <= 231 - 1

思路

这种题目属于是多解题了，我第一反应直接双指针。

讲讲我的思路吧，两个指针i、j，i在前，j在后

i去寻找s[i] < s[i+1]的位置，也就是找到一个可以进行交换的位置

j在i固定好后（找到位置后），从后向前遍历，寻找到一个比s[i]小的数，与s[i]交换，这样就能保证前半部分（到i的部分）是最小的

后半部分（i+1到末尾），需要确保也是最小的，那么就得sort排个序（或者reverse一下）

前半部分加上后半部分，转为int，结果判断是否是32位有符号数

代码

function nextGreaterElement(n: number): number {
    let s = [...n + ""]
    let l = s.length
    for (let i = l - 2; i >= 0; i--) {
        if (s[i] >= s[i + 1]) continue  // 左位比右位大，交换后的数会变小，直接跳过
        for (let j = l - 1; j > i; j--) {
            // 左位比右位小，从后向前找比s[i]大的那一位
            if (s[j] > s[i]) {
                // 交换两个
                let tmp = s[i]
                s[i] = s[j]
                s[j] = tmp
                break
            }
        }
        // 交换完后，要确保后面的部分是最小的
        let left = s.slice(0, i + 1)
        let right = s.slice(i + 1, l)
        right.sort()
        let res = parseInt(left.join('') + right.join(''))
        return res <= 2 ** 31 - 1 ? res : -1
    }
    return -1
}

7.4 最小绝对差

题目

1200. 最小绝对差

给你个整数数组 arr，其中每个元素都 不相同。

请你找到所有具有最小绝对差的元素对，并且按升序的顺序返回。

每对元素对 [a,b] 如下：

• a , b 均为数组 arr 中的元素
• a < b
• b - a 等于 arr 中任意两个元素的最小绝对差

示例 1：

输入：arr = [4,2,1,3]
输出：[[1,2],[2,3],[3,4]]

示例 2：

输入：arr = [1,3,6,10,15]
输出：[[1,3]]

示例 3：

输入：arr = [3,8,-10,23,19,-4,-14,27]
输出：[[-14,-10],[19,23],[23,27]]

提示：

• 2 <= arr.length <= 10^5
• -10^6 <= arr[i] <= 10^6

思路

先按升序排序，第一次遍历，获取最小绝对差

第二次遍历得到绝对差为最小绝对差的元素对

代码

function minimumAbsDifference(arr: number[]): number[][] {
    arr.sort((a, b) => a - b)   // 顺序排序
    // 第一次遍历，寻找最小绝对差
    let min = Number.MAX_VALUE
    for (let i = 0; i < arr.length-1; i++) {
        let cha = arr[i+1] - arr[i]
        if (cha < min) {
            min = cha
        }
    }
    // 第二次遍历，获取绝对差为最小绝对差的元素对
    let res = []
    for (let i = 0; i < arr.length-1; i++) {
        if (arr[i+1] - arr[i] == min) {
            res.push([arr[i],arr[i+1]])
        }
    }
    return res
}

7.5 我的日程安排表 I

题目

729. 我的日程安排表 I

实现一个 MyCalendar 类来存放你的日程安排。如果要添加的日程安排不会造成 重复预订 ，则可以存储这个新的日程安排。

当两个日程安排有一些时间上的交叉时（例如两个日程安排都在同一时间内），就会产生 重复预订 。

日程可以用一对整数 start 和 end 表示，这里的时间是半开区间，即 [start, end), 实数 x 的范围为， start <= x < end 。

实现 MyCalendar 类：

• MyCalendar() 初始化日历对象。
• boolean book(int start, int end) 如果可以将日程安排成功添加到日历中而不会导致重复预订，返回 true 。否则，返回 false 并且不要将该日程安排添加到日历中。

示例：

输入：
["MyCalendar", "book", "book", "book"]
[[], [10, 20], [15, 25], [20, 30]]
输出：
[null, true, false, true]

解释：
MyCalendar myCalendar = new MyCalendar();
myCalendar.book(10, 20); // return True
myCalendar.book(15, 25); // return False ，这个日程安排不能添加到日历中，因为时间 15 已经被另一个日程安排预订了。
myCalendar.book(20, 30); // return True ，这个日程安排可以添加到日历中，因为第一个日程安排预订的每个时间都小于 20 ，且不包含时间 20 。

提示：

• 0 <= start < end <= 109
• 每个测试用例，调用 book 方法的次数最多不超过 1000 次。

思路

使用公交车站的思路，理解为start时刻上车一人，end时刻下车一人

同时要保证公交车仅仅能够乘坐一个人，如果上车后多余一个人，那么就无法让其上车

要注意，输入的那个列表需要按时间排序，因为是按照时间来进行上下车的

代码

class MyCalendar {
    map: Map<number, number> = new Map()
    constructor() {
    }

    book(start: number, end: number): boolean {
        let map = this.map
        map.set(start, map.get(start) === undefined ? 1 : map.get(start) + 1)
        map.set(end, map.get(end) === undefined ? -1 : map.get(end) - 1)
        let arr = Array.from(map)
        arr.sort((a, b) => { return a[0] - b[0] }) // 按时间排序
        let tmp = 0
        for (let val of arr) {
            tmp += val[1]
            if (tmp > 1) {  // 交叉了，还原，返回false
                map.set(start, map.get(start) === undefined ? -1 : map.get(start) - 1)
                map.set(end, map.get(end) === undefined ? 1 : map.get(end) + 1)
                return false
            }
        }
        return true
    }
}

7.6 Lisp 语法解析

题目

736. Lisp 语法解析

给你一个类似 Lisp 语句的字符串表达式 expression，求出其计算结果。

表达式语法如下所示:

• 表达式可以为整数，let 表达式，add 表达式，mult 表达式，或赋值的变量。表达式的结果总是一个整数。
• (整数可以是正整数、负整数、0)
• let 表达式采用 "(let v1 e1 v2 e2 ... vn en expr)" 的形式，其中 let 总是以字符串 "let"来表示，接下来会跟随一对或多对交替的变量和表达式，也就是说，第一个变量 v1被分配为表达式 e1 的值，第二个变量 v2 被分配为表达式 e2 的值，依次类推；最终 let 表达式的值为 expr表达式的值。
• add 表达式表示为 "(add e1 e2)" ，其中 add 总是以字符串 "add" 来表示，该表达式总是包含两个表达式 e1、e2 ，最终结果是 e1 表达式的值与 e2 表达式的值之 和 。
• mult 表达式表示为 "(mult e1 e2)" ，其中 mult 总是以字符串 "mult" 表示，该表达式总是包含两个表达式 e1、e2，最终结果是 e1 表达式的值与 e2 表达式的值之 积 。
• 在该题目中，变量名以小写字符开始，之后跟随 0 个或多个小写字符或数字。为了方便，"add" ，"let" ，"mult" 会被定义为 "关键字" ，不会用作变量名。
• 最后，要说一下作用域的概念。计算变量名所对应的表达式时，在计算上下文中，首先检查最内层作用域（按括号计），然后按顺序依次检查外部作用域。测试用例中每一个表达式都是合法的。有关作用域的更多详细信息，请参阅示例。

示例 1：

输入：expression = "(let x 2 (mult x (let x 3 y 4 (add x y))))"
输出：14
解释：
计算表达式 (add x y), 在检查变量 x 值时，
在变量的上下文中由最内层作用域依次向外检查。
首先找到 x = 3, 所以此处的 x 值是 3 。

示例 2：

输入：expression = "(let x 3 x 2 x)"
输出：2
解释：let 语句中的赋值运算按顺序处理即可。

示例 3：

输入：expression = "(let x 1 y 2 x (add x y) (add x y))"
输出：5
解释：
第一个 (add x y) 计算结果是 3，并且将此值赋给了 x 。 
第二个 (add x y) 计算结果是 3 + 2 = 5 。

提示：

• 1 <= expression.length <= 2000
• exprssion 中不含前导和尾随空格
• expressoin 中的不同部分（token）之间用单个空格进行分隔
• 答案和所有中间计算结果都符合 32-bit 整数范围
• 测试用例中的表达式均为合法的且最终结果为整数

思路

纯纯的困难题，思路其实很简单，要么dfs要么就分治（其实都算分治吧），写法上的区别存粹就是自己定义属性上的区别

我这里借鉴了高阅读量题解的思路，直接一整个复现了一下，debug搞了20多分钟，纯纯的细节题

自己还是理一遍思路吧：

对于一个expression表达式，我们首先进行一个分解

例如"(let a 114 b 514 (add a b))"，我们应该分解成两个部分，let部分和add部分

• let部分我们叫做定义部分
• add部分叫做剩余expression部分

我们在定义部分，对其中的变量进行map的映射赋值操作

在剩余expression部分进行最终返回值的计算

例如上面的例子就可以分解成

• let a 114 b 514
• return (add a b)

对于剩余的expression部分，我们又可以对其进行分解，分解成定义部分和剩余部分，直到所有的值被计算完，就返回结果

代码

function evaluate(expression: string): number {
    const LET: string = 'let'
    const ADD: string = 'add'
    // const MULT: string = 'mult'

    /**
     * 对表达式进行分解
     * 
     * @param expr 表达式
     * @returns 分解后的表达式
     */
    const parseExpress = (expr: string) => {
        expr = expr.substring(1, expr.length - 1)
        let res: string[] = []
        let left: number = 0    // 左指针
        let right: number = 0   // 右指针
        let len = expr.length
        while (right < len) {
            if (expr[right] === ' ') {
                // 是空格，那么可以分割成let v1 e1 和 一部分expr
                res.push(expr.substring(left, right))
                left = right + 1    // 左指针指向下一个内容
            } else if (expr[right] === '(') {
                // 是左括号，证明遍历到了expr的部分，进行括号统计，找到当前携带括号的expr的作用域
                let cnt = 0
                while (right < len) {
                    if (expr[right] === '(') cnt++
                    else if (expr[right] === ')') cnt--
                    right++
                    if (cnt === 0) break    // cnt再次为0表示括号统计完毕
                }
                res.push(expr.substring(left, right))
                left = right + 1
            }
            right++     // 右指针继续向下遍历
        }
        if (left < len) {   // 如果没有出现左括号，补充剩余部分x
            res.push(expr.substring(left))
        }
        // console.log(res)
        return res
    }

    /**
     * 计算表达式
     * 
     * @param expr 表达式
     * @param preScope 上一个传入的作用域的map
     * @returns 计算后的结果
     */
    const calc = (expr: string, preScope: Map<string, number>) => {
        let exprs: string[] = parseExpress(expr)
        let len = exprs.length
        // 如果是let，let的形式都是 let v1 e1 .... expr
        if (exprs[0] === LET) {
            // 深拷贝一份作用域文件，作为当前的新作用域，这个新作用域可以在之后进行改变
            let curScope = new Map<string, number>()
            Object.assign(curScope, preScope)
            // 对后面传入的变量进行解析，解析每个v，间隔2为下一个v
            for (let i = 1; i < len - 2; i += 2) {
                let e = 0
                if (exprs[i + 1][0] === '(') {
                    // 如果当前变量的值，是一个表达式，那么计算下一个表达式的值先
                    e = calc(exprs[i + 1], curScope)
                } else {
                    // 如果当前变量的值是上一个作用域存在的，直接读取
                    if (curScope[exprs[i + 1]] !== undefined) e = curScope[exprs[i + 1]]
                    // 否则就是单纯定义的数值
                    else e = parseInt(exprs[i + 1])
                }
                // console.log(e)
                // 将e给存储到当前的作用域中
                curScope[exprs[i]] = e
            }
            // console.log(curScope)
            // 解析let的最后部分的expr
            if (exprs[len - 1][0] === '(') {
                // 如果最后的expr是一个表达式，计算这个表达式，因为之前最新的变量都被存储到了curScope中，直接传入就可以得到最后的答案
                return calc(exprs[len - 1], curScope)
            } else {
                // 如果是单纯的一个变量字母，必定存在作用域中，否则就是单纯的一个值
                return curScope[exprs[len - 1]] !== undefined ? curScope[exprs[len - 1]] : parseInt(exprs[len - 1])
            }
        } else {
            // 如果是add或者mult，进行计算
            // 首先要得到两个将要被计算的变量
            let ans = [0,0]
            // console.log(preScope)
            ans[0] = exprs[1][0] === '(' ? calc(exprs[1], preScope) : (preScope[exprs[1]] !== undefined ? preScope[exprs[1]] : parseInt(exprs[1]))
            ans[1] = exprs[2][0] === '(' ? calc(exprs[2], preScope) : (preScope[exprs[2]] !== undefined ? preScope[exprs[2]] : parseInt(exprs[2]))
            // console.log(ans)
            return exprs[0] === ADD ? ans[0] + ans[1] : ans[0] * ans[1]
        }
    }

    return calc(expression, new Map<string, number>())
}

7.7 单词替换

题目

648. 单词替换

在英语中，我们有一个叫做 词根(root) 的概念，可以词根后面添加其他一些词组成另一个较长的单词——我们称这个词为 继承词(successor)。例如，词根an，跟随着单词 other(其他)，可以形成新的单词 another(另一个)。

现在，给定一个由许多词根组成的词典 dictionary 和一个用空格分隔单词形成的句子 sentence。你需要将句子中的所有继承词用词根替换掉。如果继承词有许多可以形成它的词根，则用最短的词根替换它。

你需要输出替换之后的句子。

示例 1：

输入：dictionary = ["cat","bat","rat"], sentence = "the cattle was rattled by the battery"
输出："the cat was rat by the bat"

示例 2：

输入：dictionary = ["a","b","c"], sentence = "aadsfasf absbs bbab cadsfafs"
输出："a a b c"

提示：

• 1 <= dictionary.length <= 1000
• 1 <= dictionary[i].length <= 100
• dictionary[i] 仅由小写字母组成。
• 1 <= sentence.length <= 10^6
• sentence 仅由小写字母和空格组成。
• sentence 中单词的总量在范围 [1, 1000] 内。
• sentence 中每个单词的长度在范围 [1, 1000] 内。
• sentence 中单词之间由一个空格隔开。
• sentence 没有前导或尾随空格。

思路

纯纯的思路很简单的题目，Java类语言如果带了startWith()这类的方法，直接暴力就能过了，数据量没那么大（说的就是我）

但是为了学一下字典树，在用暴力过了一遍之后还是敲了一下字典树

先说说暴力的思路吧，30s内就能想出来

• 先给sentence split处理一下，获得一个string数组
• 对这个string数组进行遍历
• 遍历的过程中，对dictionary进行遍历，看看这个string是否是具有词根的
• 如果具有词根，记录下最短的词根（当然这里可以直接在遍历dictionary之前，对dictionary进行sort排序）
• 将当前string变为词根
• 返回处理后的字符串

再来讲讲字典树的思路

• TrieNode类有两个成员变量
  • children，一个TrieNode数组，用来存放当前节点的下一个26个字母
  • isEnd，是否插完过一个string
• 对于所有的dictionary中的dic，全部插入到一个新的TrieNode中
• 对于所有的从sentence中获取的words，遍历一遍，检查是否其前缀是否存在字典树中，存在就返回前缀，否则就返回自己
• 返回所有经过字典树check的结果

代码

暴力：(没有进行sort优化，需要两个for循环到底，无法在第二个for循环break，可以优化，但是我懒)

function replaceWords(dictionary: string[], sentence: string): string {
    let words = sentence.split(' ')
    let len = words.length
    for (let i = 0; i < len; i++) {
        let minLen = 101
        let minDic = words[i]
        for (let dic of dictionary) {
            if (words[i].startsWith(dic)) {
                if (dic.length < minLen) {
                    minLen = dic.length
                    minDic =dic
                }
            }
        }
        words[i] = minDic
    }
    return words.join(" ")
}

字典树：

function replaceWords(dictionary: string[], sentence: string): string {
    let words = sentence.split(' ')
    let node = new TrieNode()
    for (let dic of dictionary) node.insert(dic)    // 词前缀插入字典树
    for (let i = 0; i < words.length; i++) {
        words[i] = node.check(words[i])     // 进行替换
    }
    return words.join(" ")
}

class TrieNode{
    private child: TrieNode[]
    private isEnd: boolean
    constructor() {
        this.isEnd = false
        this.child = new Array<TrieNode>(26)
    }

    insert(str: string) {
        let node: TrieNode = this
        for(let i = 0; i < str.length; i++) {
            let idx = str[i].charCodeAt(0) - 'a'.charCodeAt(0)
            if (node.child[idx] == undefined) {
                node.child[idx] = new TrieNode()
            }
            node = node.child[idx]
        }
        node.isEnd = true  // 到此结束
    }

    check(str: string) {
        let node: TrieNode = this
        let res = ''
        for (let i = 0; i < str.length; i++) {
            let idx = str[i].charCodeAt(0) - 'a'.charCodeAt(0)
            if (node.child[idx] === undefined) break
            res += str[i]
            node = node.child[idx]
            if (node.isEnd) return res
        }
        return str
    }
}

貌似也没快很多，但是内存开销必然增大很多

7.8 玩筹码

题目

1217. 玩筹码

有 n 个筹码。第 i 个筹码的位置是 position[i] 。

我们需要把所有筹码移到同一个位置。在一步中，我们可以将第 i 个筹码的位置从 position[i] 改变为:

• position[i] + 2 或 position[i] - 2 ，此时 cost = 0
• position[i] + 1 或 position[i] - 1 ，此时 cost = 1

返回将所有筹码移动到同一位置上所需要的 最小代价 。

示例 1：

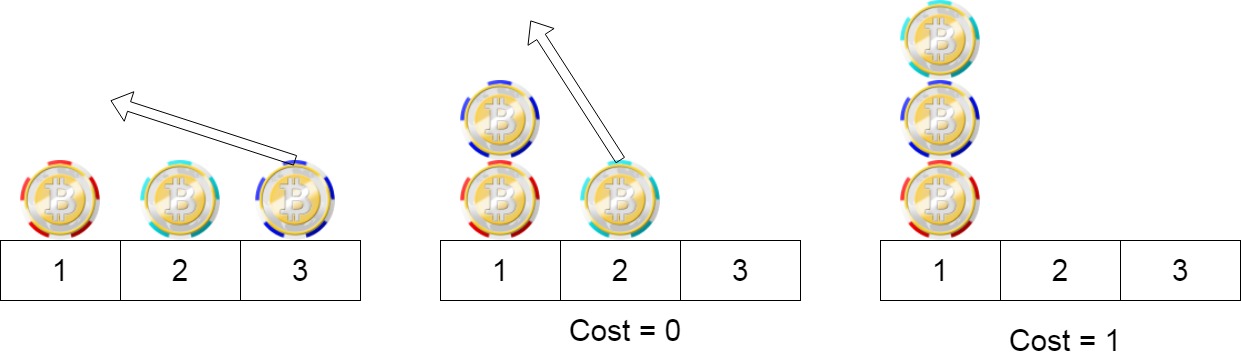
输入：position = [1,2,3]
输出：1
解释：第一步:将位置3的筹码移动到位置1，成本为0。
第二步:将位置2的筹码移动到位置1，成本= 1。
总成本是1。

示例 2：

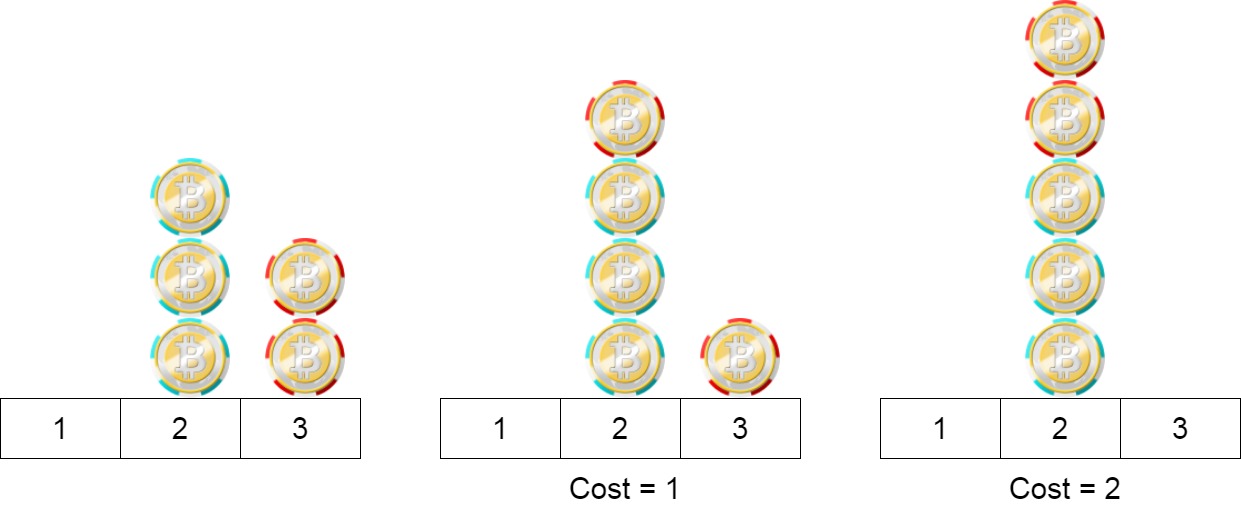
输入：position = [2,2,2,3,3]
输出：2
解释：我们可以把位置3的两个筹码移到位置2。每一步的成本为1。总成本= 2。

示例 3:

输入：position = [1,1000000000]
输出：1

提示：

• 1 <= chips.length <= 100
• 1 <= chips[i] <= 10^9

思路

直接贪心。发现偶数移动不消耗代价，可以将所有的偶数坐标全部移动到同一个位置而不消耗代价，同理，将所有的奇数位移动到同一位置，也不消耗代价

最后的代价就是两种情况

• 将偶数堆移动到奇数堆头上，消耗代价为偶数堆的个数
• 将奇数堆移动到偶数堆头上，消耗代价为奇数堆的个数

代码

function minCostToMoveChips(position: number[]): number {
    let a = 0, b = 0
    for (let i = 0; i < position.length; i++) {
        (position[i] & 1) === 1 ? a++ : b++
    }
    return Math.min(a, b)
}

吐槽一句，ts对位运算的优化不太行，执行速度有点慢

7.9 最长的斐波那契子序列的长度

题目

873. 最长的斐波那契子序列的长度

如果序列 X_1, X_2, ..., X_n 满足下列条件，就说它是 斐波那契式 的：

• n >= 3
• 对于所有 i + 2 <= n，都有 X_i + X_{i+1} = X_{i+2}

给定一个严格递增的正整数数组形成序列 arr ，找到 arr 中最长的斐波那契式的子序列的长度。如果一个不存在，返回 0 。

（回想一下，子序列是从原序列 arr 中派生出来的，它从 arr 中删掉任意数量的元素（也可以不删），而不改变其余元素的顺序。例如， [3, 5, 8] 是 [3, 4, 5, 6, 7, 8] 的一个子序列）

示例 1：

输入: arr = [1,2,3,4,5,6,7,8]
输出: 5
解释: 最长的斐波那契式子序列为 [1,2,3,5,8] 。

示例 2：

输入: arr = [1,3,7,11,12,14,18]
输出: 3
解释: 最长的斐波那契式子序列有 [1,11,12]、[3,11,14] 以及 [7,11,18] 。

提示：

• 3 <= arr.length <= 1000
• 1 <= arr[i] < arr[i + 1] <= 10^9

思路

迭代的思路，暴力枚举所有的可能性

先用一个set记录arr中出现过的元素

双重for循环判断pre + next得到的sum是否出现再set中，如果出现了，那就一条链继续向下走，走到尽头

每次走到尽头判读该链是否是当前最长的，进行状态更新

最后返回最长的那条斐波那契链的长度

代码

function lenLongestFibSubseq(arr: number[]): number {
    let set = new Set<number>()
    arr.forEach(item => set.add(item))   // 记录所有的元素
    let len = arr.length
    let maxLen = -1
    for (let i = 0; i < len-1; i++) {
        for (let j = i+1; j < len; j++) {
            let tl = 2
            let pre = arr[i]
            let next = arr[j]
            let sum = pre + next
            while (set.has(sum)) {
                // console.log(pre+' + ' +next +' = ' +sum)
                tl++
                pre = next
                next = sum
                sum = pre + next
            }
            maxLen = Math.max(maxLen, tl)
        }
    }
    return maxLen === 2 ? 0 : maxLen
}

7.10 摘樱桃

题目

741. 摘樱桃

一个N x N的网格(grid) 代表了一块樱桃地，每个格子由以下三种数字的一种来表示：

• 0 表示这个格子是空的，所以你可以穿过它。
• 1 表示这个格子里装着一个樱桃，你可以摘到樱桃然后穿过它。
• -1 表示这个格子里有荆棘，挡着你的路。

你的任务是在遵守下列规则的情况下，尽可能的摘到最多樱桃：

• 从位置 (0, 0) 出发，最后到达 (N-1, N-1) ，只能向下或向右走，并且只能穿越有效的格子（即只可以穿过值为0或者1的格子）；
• 当到达 (N-1, N-1) 后，你要继续走，直到返回到 (0, 0) ，只能向上或向左走，并且只能穿越有效的格子；
• 当你经过一个格子且这个格子包含一个樱桃时，你将摘到樱桃并且这个格子会变成空的（值变为0）；
• 如果在 (0, 0) 和 (N-1, N-1) 之间不存在一条可经过的路径，则没有任何一个樱桃能被摘到。

示例 1:

输入: grid =
[[0, 1, -1],
 [1, 0, -1],
 [1, 1,  1]]
输出: 5
解释： 
玩家从（0,0）点出发，经过了向下走，向下走，向右走，向右走，到达了点(2, 2)。
在这趟单程中，总共摘到了4颗樱桃，矩阵变成了[[0,1,-1],[0,0,-1],[0,0,0]]。
接着，这名玩家向左走，向上走，向上走，向左走，返回了起始点，又摘到了1颗樱桃。
在旅程中，总共摘到了5颗樱桃，这是可以摘到的最大值了。

说明:

• grid 是一个 N * N 的二维数组，N的取值范围是1 <= N <= 50。
• 每一个 grid[i][j] 都是集合 {-1, 0, 1}其中的一个数。
• 可以保证起点 grid[0][0] 和终点 grid[N-1][N-1] 的值都不会是 -1。

思路

纯纯的坐牢题，第一想法是深搜，如果过不了准备剪枝。

后来发现，一次从(0,0)到(n-1, n-1)再从(n-1,n-1)到(0,0)，两次的最优解是 ！= 全局最优解的。

看了大部分题解，最好理解的思路就是，可以看成两个点同时从(0,0)走向(n-1,n-1)。三维动态规划（其实是由四维动态规划转过来了）

四维dp的思路是，dp[i1][j1][i2][j2]，表示点a走到(i1,j1)和点b走到(i2,j2)的最多樱桃数。同时一共有4种走法

• a右 b右 dp[i1][j1-1][i2][j2-1]
• a右 b下 dp[i1][j1-1][i2-1][j2]
• a下 b右 dp[i1-1][j1][i2][j2-1]
• a下 b下 dp[i1-1][j1][i2-1][j2]

可以得到状态转义方程

• dp[i1][j1][i2][j2] = max(dp[i1][j1-1][i2][j2-1], dp[i1][j1-1][i2-1][j2], dp[i1-1][j1][i2][j2-1], dp[i1-1][j1][i2-1][j2]) + grid[i1][j1] + grid[i2][j2]
• 如果(i1,j1)和(i2,j2)是同一个点，那么就少加一个
• 如果(i1,j1)和(i2,j2)是-1，直接遍历下一个状态

有了上述四维dp的思路后，我们可以简化成三维，因为两个点每次走的路程是一样的，假设a走了k步，那么b也走了k步，同时我们直到a的行数i1，就可以得到a的列数j1 = k - i1，同理，b的行和列也能得到

也就是我们将四维的两个坐标，简化成了步数 + 行数的形式，减少了一个维度的使用，减少内存消耗。这三维的思路来自这篇题解

三维dp的思路我写在下面的代码里了，不得不说这种题目虽然知道是哪一类的题，但是真要敲出来还是挺难的（对于我来说。。）

代码

function cherryPickup(grid: number[][]): number {
    const INF = -0x3f3f3f3f
    let dp: number[][][] = new Array<Array<Array<number>>>()
    let N = grid.length
    // 为了方便，将grid的横纵坐标从1开始理解
    // 初始化三维数组
    // 先右下走，再左上返回，其实等价于，两个点a，b同时向右下走
    // 定义k = x1 + y1 == x 2+ y2，表示走的步数
    // dp[k][i1][i2] 表示走了k步，a在i1行，b在i2行的最多樱桃数
    // 因为a和b是同时走，k=1表示a走了1步，b也走了1步
    // 那么dp[2][1][1] = grid[0][0]
    // 最终返回dp[2n][n][n]
    for (let i = 0; i <= 2 * N; i++) {
        dp[i] = new Array<Array<number>>()
        for (let j = 0; j <= N; j++) {
            dp[i][j] = new Array<number>()
            for (let k = 0; k <= N; k++) {
                dp[i][j][k] = INF
            }
        }
    }
    dp[2][1][1] = grid[0][0]    // 状态开始
    for (let k = 3; k <= 2 * N; k++) {
        for (let i1 = 1; i1 <= N; i1++) {
            for (let i2 = 1; i2 <= N; i2++) {
                let j1 = k - i1
                let j2 = k - i2
                // 边界判断
                if (j1 <= 0 || j1 > N || j2 <= 0 || j2 > N) continue
                let A = grid[i1 - 1][j1 - 1]    // 在i1行 j1列的点a
                let B = grid[i2 - 1][j2 - 1]    // 在（i2，j2）的点b
                // 是否可走
                if (A == -1 || B == -1) continue
                // 4中可能的走法
                // 1. a向右，b向右(行不变)
                let case1 = dp[k - 1][i1][i2]
                // 2. a向右，b向下(b的行+1)，因为计算的是从哪里来，所以是i2-1
                let case2 = dp[k - 1][i1][i2 - 1]
                // 3. a向下，b向右
                let case3 = dp[k - 1][i1 - 1][i2]
                // 4. ab都向下
                let case4 = dp[k - 1][i1 - 1][i2 - 1]
                // 找到上述4种情况最大的解法
                let curMax = Math.max(case1, case2, case3, case4)
                // 判断是否到同一点，如果是同一个点就只能加一次
                if (i1 == i2) {
                    curMax += A
                } else {
                    curMax += A + B
                }
                dp[k][i1][i2] = curMax
            }
        }
    }
    return dp[2 * N][N][N] <= 0 ? 0 : dp[2 * N][N][N]
}

7.11 实现一个魔法字典

题目

676. 实现一个魔法字典

设计一个使用单词列表进行初始化的数据结构，单词列表中的单词 互不相同 。 如果给出一个单词，请判定能否只将这个单词中一个字母换成另一个字母，使得所形成的新单词存在于你构建的字典中。

实现 MagicDictionary 类：

• MagicDictionary() 初始化对象
• void buildDict(String[] dictionary) 使用字符串数组 dictionary 设定该数据结构，dictionary 中的字符串互不相同
• bool search(String searchWord) 给定一个字符串 searchWord ，判定能否只将字符串中 一个 字母换成另一个字母，使得所形成的新字符串能够与字典中的任一字符串匹配。如果可以，返回 true ；否则，返回 false 。

示例：

输入
["MagicDictionary", "buildDict", "search", "search", "search", "search"]
[[], [["hello", "leetcode"]], ["hello"], ["hhllo"], ["hell"], ["leetcoded"]]
输出
[null, null, false, true, false, false]

解释
MagicDictionary magicDictionary = new MagicDictionary();
magicDictionary.buildDict(["hello", "leetcode"]);
magicDictionary.search("hello"); // 返回 False
magicDictionary.search("hhllo"); // 将第二个 'h' 替换为 'e' 可以匹配 "hello" ，所以返回 True
magicDictionary.search("hell"); // 返回 False
magicDictionary.search("leetcoded"); // 返回 False

提示：

• 1 <= dictionary.length <= 100
• 1 <= dictionary[i].length <= 100
• dictionary[i] 仅由小写英文字母组成
• dictionary 中的所有字符串 互不相同
• 1 <= searchWord.length <= 100
• searchWord 仅由小写英文字母组成
• buildDict 仅在 search 之前调用一次
• 最多调用 100 次 search

思路

因为前几天做过字典树的题目，所以直接想用字典树来做了。

这里需要变化一下check方法

我第一次开始写这题的时候，就像直接用迭代来写出来，后来越写越复杂，直到成了一坨屎山，直接放弃了，换成递归执行

思路是这样的

1. 把dic里的单词全部插入到字典树中
2. 使用check进行检查
3. check需要传入四个参数，当前字典树节点、单词、当前遍历的位置、是否修改过
4. 如果遍历完了，就返回 是否修改过 && 是否到了单词结尾
5. 如果没遍历完，就去查看当前遍历到的位置的字符是否出现在字典树中
6. 如果出现在字典树中，向下挖掘。chekc下一个位置的字符
7. 如果没出现在树中，从a到z暴力改变当前的字符，查看改变后是否可以check成功
8. 如果上述操作都无效，返回false

代码

class MagicDictionary {
    node: TrieNode
    constructor() {
        this.node = new TrieNode()
    }

    buildDict(dictionary: string[]): void {
        for (let dic of dictionary) {
            this.node.insert(this.node, dic)
        }
    }

    search(searchWord: string): boolean {
        return this.node.check(this.node, searchWord, 0, false)
    }
}

class TrieNode {
    children: TrieNode[]
    isEnd: boolean
    constructor() {
        this.isEnd = false
        this.children = new Array<TrieNode>(26)
    }

    insert(node: TrieNode, str: string) {
        let len = str.length
        for (let i = 0; i < len; i++) {
            let idx = str[i].charCodeAt(0) - 'a'.charCodeAt(0)
            if (node.children[idx] === undefined) {
                node.children[idx] = new TrieNode()
            }
            node = node.children[idx]
        }
        node.isEnd = true   // 结束
    }

    check(node: TrieNode, str: string, idx: number, isChanged: boolean) {
        let len = str.length
        if (idx === len) {
            // 全部遍历完成
            return isChanged && node.isEnd
        }
        let i = str[idx].charCodeAt(0) - 'a'.charCodeAt(0)
        // 匹配到了字符，就向下挖掘
        if (node.children[i] !== undefined) {
            if (this.check(node.children[i], str, idx + 1, isChanged)) {
                return true
            }
        }
        // 没匹配到，就去尝试改变
        if (!isChanged) {
            isChanged = true
            for (let start = 0; start < 26; start++) {
                if (start === i) continue   // 跳过自己
                if (node.children[start] !== undefined) {
                    // 爆破到的字符存在，且下一个字符也存在
                    if (this.check(node.children[start], str, idx + 1, isChanged))
                        return true
                }
            }
        }
        return false
    }
}

7.12 奇数值单元格的数目

题目

1252. 奇数值单元格的数目

给你一个 m x n 的矩阵，最开始的时候，每个单元格中的值都是 0。

另有一个二维索引数组 indices，indices[i] = [ri, ci] 指向矩阵中的某个位置，其中 ri 和 ci 分别表示指定的行和列（从 0 开始编号）。

对 indices[i] 所指向的每个位置，应同时执行下述增量操作：

1. ri 行上的所有单元格，加 1 。
2. ci 列上的所有单元格，加 1 。

给你 m、n 和 indices 。请你在执行完所有 indices 指定的增量操作后，返回矩阵中 奇数值单元格 的数目。

示例 1：

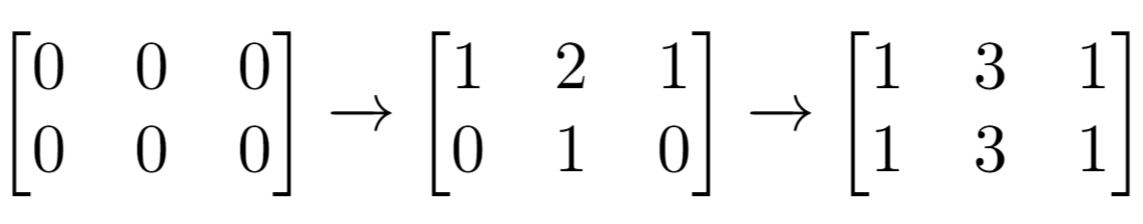
输入：m = 2, n = 3, indices = [[0,1],[1,1]]
输出：6
解释：最开始的矩阵是 [[0,0,0],[0,0,0]]。
第一次增量操作后得到 [[1,2,1],[0,1,0]]。
最后的矩阵是 [[1,3,1],[1,3,1]]，里面有 6 个奇数。

示例 2：

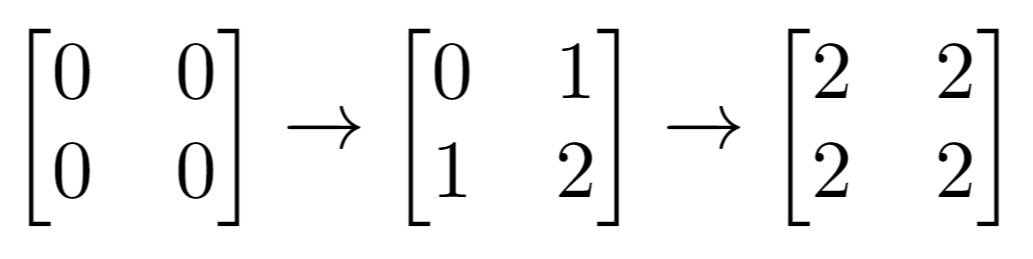
输入：m = 2, n = 2, indices = [[1,1],[0,0]]
输出：0
解释：最后的矩阵是 [[2,2],[2,2]]，里面没有奇数。

提示：

• 1 <= m, n <= 50
• 1 <= indices.length <= 100
• 0 <= ri < m
• 0 <= ci < n

**进阶：**你可以设计一个时间复杂度为 O(n + m + indices.length) 且仅用 O(n + m) 额外空间的算法来解决此问题吗？

思路

直接暴力，能少用脑子就少用一点

代码

function oddCells(m: number, n: number, indices: number[][]): number {
    let matrix: number[][] = new Array<Array<number>>()
    for (let i = 0; i < m; i++) {
        matrix[i] = new Array(n)
        for (let j = 0; j < n; j++) {
            matrix[i][j] = 0
        }
    }
    indices.forEach(item => {
        let row = item[0]
        for (let i = 0; i < n; i++) {
            matrix[row][i]++
        }
        let col = item[1]
        for (let i = 0; i < m; i++) {
            matrix[i][col]++
        }
    })
    let res = 0
    for (let arr of matrix) {
        for (let it of arr) {
            if (it % 2 !== 0) {
                res++
            }
        }
    }
    return res
}

7.13 行星碰撞

题目

735. 行星碰撞

给定一个整数数组 asteroids，表示在同一行的行星。

对于数组中的每一个元素，其绝对值表示行星的大小，正负表示行星的移动方向（正表示向右移动，负表示向左移动）。每一颗行星以相同的速度移动。

找出碰撞后剩下的所有行星。碰撞规则：两个行星相互碰撞，较小的行星会爆炸。如果两颗行星大小相同，则两颗行星都会爆炸。两颗移动方向相同的行星，永远不会发生碰撞。

示例 1：

输入：asteroids = [5,10,-5]
输出：[5,10]
解释：10 和 -5 碰撞后只剩下 10 。 5 和 10 永远不会发生碰撞。

示例 2：

输入：asteroids = [8,-8]
输出：[]
解释：8 和 -8 碰撞后，两者都发生爆炸。

示例 3：

输入：asteroids = [10,2,-5]
输出：[10]
解释：2 和 -5 发生碰撞后剩下 -5 。10 和 -5 发生碰撞后剩下 10 。

思路

直接模拟，因为两个相同方向的行星是不会碰撞的，我们给list填充向右行驶的行星，如果是碰到了向左的行星，会有如下几种情况：

1. 若list不为空，同时向左行星大于list中遍历到的当前向右行星的大小，那么向左行星直接把向右行星给创爆炸，list删除这个右行星，继续遍历下一个向右行星
2. 若list不为空，同时向左行星 == list中当前遍历到的右行星大小，两个行星都炸了，list删除这个右行星
3. 左行星小于list中遍历到的右行星，左行星直接创碎了，找到下一个左行星来判断
4. 若list为空，或者list中已经存在了左行星，那么左行星直接加入到list中

最后直接返回list就是我们要的答案

代码

当天用的kotlin写的，就直接贴上来吧，懒得再用ts写一遍了

import kotlin.math.abs

class Solution {
    fun asteroidCollision(asteroids: IntArray): IntArray {
        val list = mutableListOf<Int>()
        for (asteroid in asteroids) {
            if (asteroid > 0) list += asteroid
            else {
                while (list.isNotEmpty() && list.last() > 0 && list.last() < abs(asteroid)) {
                    list.removeAt(list.size-1)
                } 
                if (list.isNotEmpty() && list.last() > 0 && list.last() == abs(asteroid)) {
                    list.removeAt(list.size-1)
                } else if (list.isEmpty() || list.last() < 0) {
                    list += asteroid
                }
            }
        }
        return list.toIntArray()
    }
}

7.14 前缀和后缀搜索

题目

745. 前缀和后缀搜索

设计一个包含一些单词的特殊词典，并能够通过前缀和后缀来检索单词。

实现 WordFilter 类：

• WordFilter(string[] words) 使用词典中的单词 words 初始化对象。
• f(string pref, string suff) 返回词典中具有前缀 prefix 和后缀 suff 的单词的下标。如果存在不止一个满足要求的下标，返回其中 最大的下标 。如果不存在这样的单词，返回 -1 。

示例：

输入
["WordFilter", "f"]
[[["apple"]], ["a", "e"]]
输出
[null, 0]
解释
WordFilter wordFilter = new WordFilter(["apple"]);
wordFilter.f("a", "e"); // 返回 0 ，因为下标为 0 的单词：前缀 prefix = "a" 且 后缀 suff = "e" 。

提示：

• 1 <= words.length <= 104
• 1 <= words[i].length <= 7
• 1 <= pref.length, suff.length <= 7
• words[i]、pref 和 suff 仅由小写英文字母组成
• 最多对函数 f 执行 104 次调用

思路

思路肯定是字典树，只不过需要考虑两棵树

• 第一颗是前缀树
• 第二颗时后缀树

在插入的时候，将每个word插入前缀树，word的reverse插入后缀树

每个数有一个idx集合用来存放前缀（后缀）对应的word的坐标

当两棵树都找到的时候，将两个idx集合拿出来从后向前遍历，第一次相同的坐标就是最大坐标

我本来时向基于两棵树化简的，直接用特殊字符 { 给前缀和后缀隔开，其实思路是一样的，只不过在插入的时候就把idx取到了。这样的好处就是，只用了一棵树，但是缺点是，会把word的所有情况都给插进去

代码

class WordFilter {
    node: TrieNode
    constructor(words: string[]) {
        this.node = new TrieNode()
        let index = 0   // 当前words遍历的下标
        words.forEach(word => {
            let len = word.length
            for (let i = 0; i < len; i++) {
                let behind = word.substring(i, len)
                // 插入 后缀 + { + word 的行驶
                let tmp = behind + '{' + word
                // console.log(tmp)
                this.node.insert(tmp, index)
            }
            index++
        })
    }

    f(pref: string, suff: string): number {
        return this.node.search(suff + "{" + pref)
    }
}

class TrieNode {
    child: TrieNode[]
    idx: number
    isEnd: boolean
    constructor() {
        this.child = new Array<TrieNode>(27)    // 给字符 ”{“ 一个位置
        this.idx = -1
        this.isEnd = false
    }

    insert(str: string, index: number) {
        let node: TrieNode = this
        let len = str.length
        for (let i = 0; i < len; i++) {
            let idx = str[i].charCodeAt(0) - 'a'.charCodeAt(0)
            if (node.child[idx] === undefined) {
                node.child[idx] = new TrieNode()
            }
            node = node.child[idx]
            node.idx = index
        }
        node.isEnd = true
    }

    search(str: string): number {
        let node: TrieNode = this
        let len = str.length
        for (let i = 0; i < len; i++) {
            let idx = str[i].charCodeAt(0) - 'a'.charCodeAt(0)
            if (node.child[idx] === undefined) {
                return -1
            }
            node = node.child[idx]
        }
        return node.idx
    }
}

7.15 四叉树交集

题目

558. 四叉树交集

二进制矩阵中的所有元素不是 0 就是 1 。

给你两个四叉树，quadTree1 和 quadTree2。其中 quadTree1 表示一个 n * n 二进制矩阵，而 quadTree2 表示另一个 n * n 二进制矩阵。

请你返回一个表示 n * n 二进制矩阵的四叉树，它是 quadTree1 和 quadTree2 所表示的两个二进制矩阵进行 按位逻辑或运算 的结果。

注意，当 isLeaf 为 False 时，你可以把 True 或者 False 赋值给节点，两种值都会被判题机制 接受 。

四叉树数据结构中，每个内部节点只有四个子节点。此外，每个节点都有两个属性：

• val：储存叶子结点所代表的区域的值。1 对应 True，0 对应 False；
• isLeaf: 当这个节点是一个叶子结点时为 True，如果它有 4 个子节点则为 False 。

class Node {
    public boolean val;
    public boolean isLeaf;
    public Node topLeft;
    public Node topRight;
    public Node bottomLeft;
    public Node bottomRight;
}

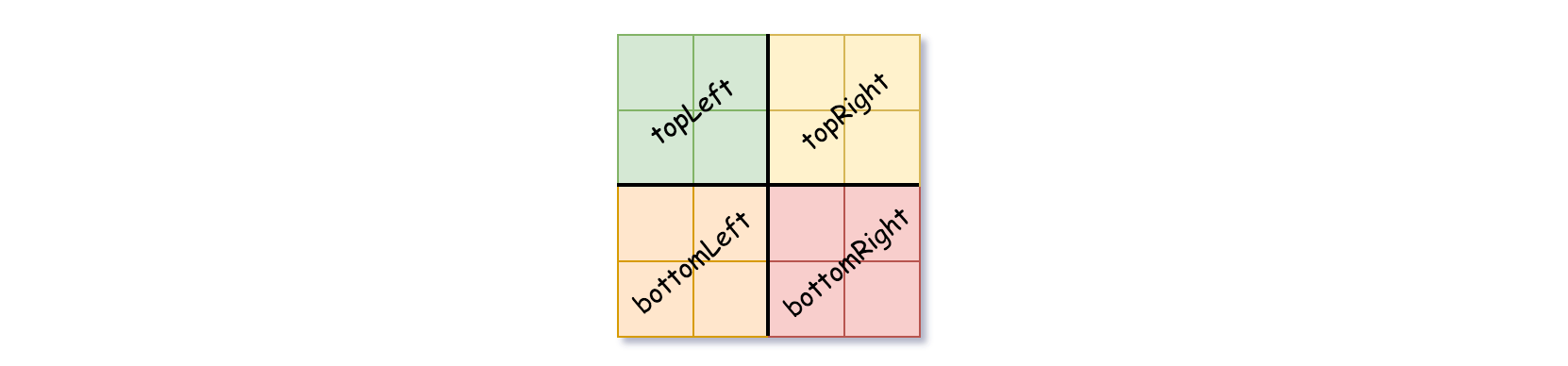
我们可以按以下步骤为二维区域构建四叉树：

1. 如果当前网格的值相同（即，全为 0 或者全为 1），将 isLeaf 设为 True ，将 val 设为网格相应的值，并将四个子节点都设为 Null 然后停止。
2. 如果当前网格的值不同，将 isLeaf 设为 False， 将 val 设为任意值，然后如下图所示，将当前网格划分为四个子网格。
3. 使用适当的子网格递归每个子节点。

如果你想了解更多关于四叉树的内容，可以参考 wiki 。

四叉树格式：

输出为使用层序遍历后四叉树的序列化形式，其中 null 表示路径终止符，其下面不存在节点。

它与二叉树的序列化非常相似。唯一的区别是节点以列表形式表示 [isLeaf, val] 。

如果 isLeaf 或者 val 的值为 True ，则表示它在列表 [isLeaf, val] 中的值为 1 ；如果 isLeaf 或者 val 的值为 False ，则表示值为 0 。

示例 1：

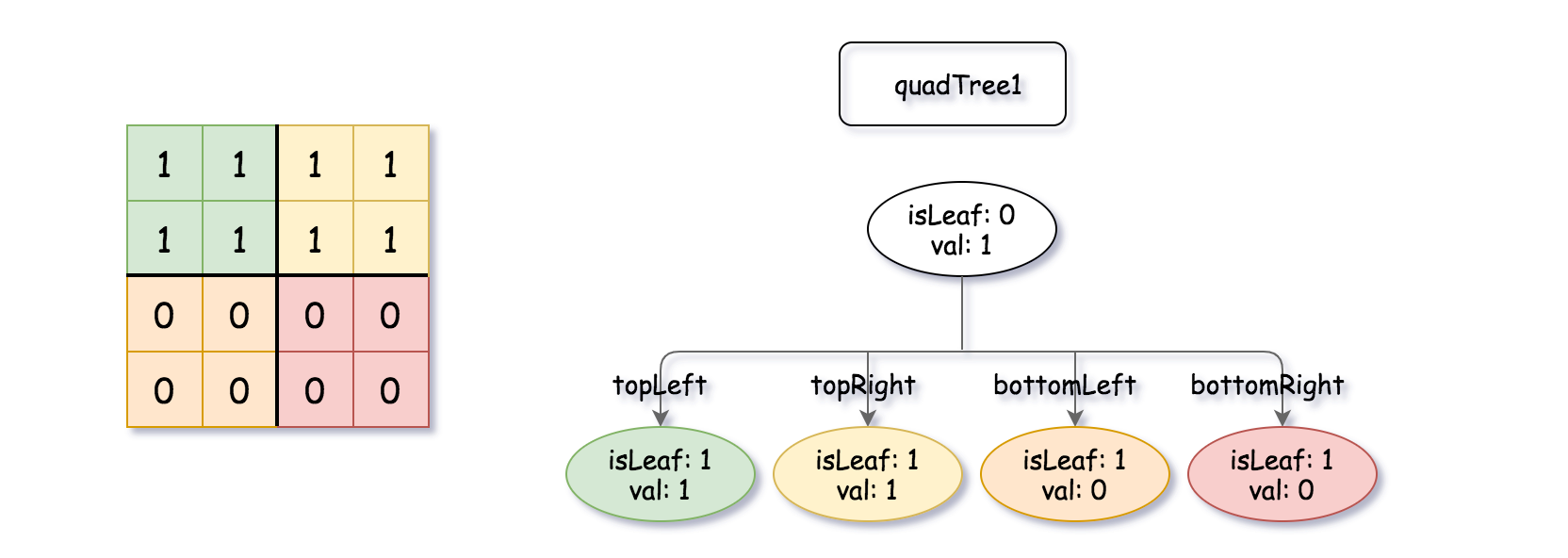
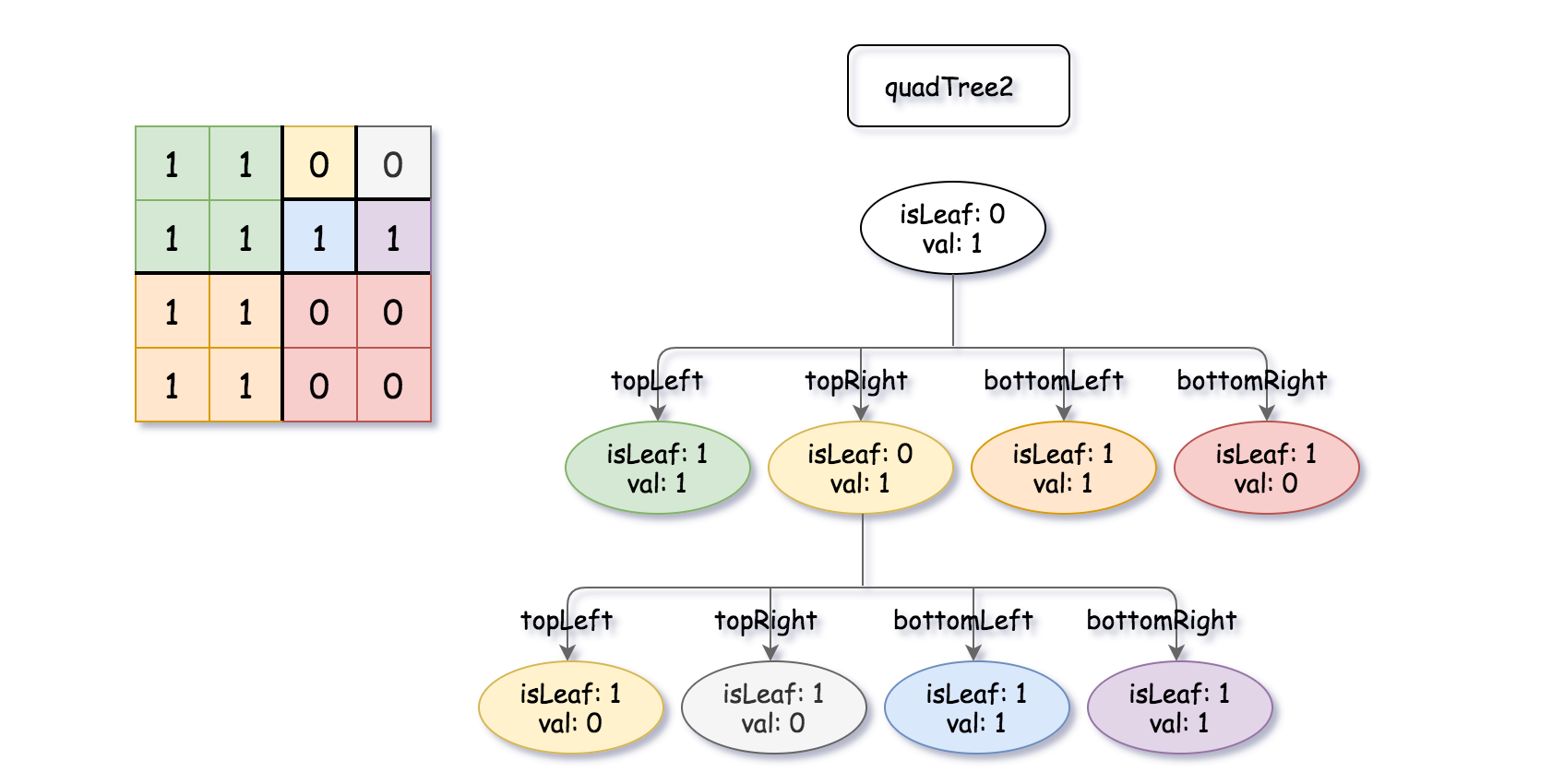
输入：quadTree1 = [[0,1],[1,1],[1,1],[1,0],[1,0]]
, quadTree2 = [[0,1],[1,1],[0,1],[1,1],[1,0],null,null,null,null,[1,0],[1,0],[1,1],[1,1]]
输出：[[0,0],[1,1],[1,1],[1,1],[1,0]]
解释：quadTree1 和 quadTree2 如上所示。由四叉树所表示的二进制矩阵也已经给出。
如果我们对这两个矩阵进行按位逻辑或运算，则可以得到下面的二进制矩阵，由一个作为结果的四叉树表示。
注意，我们展示的二进制矩阵仅仅是为了更好地说明题意，你无需构造二进制矩阵来获得结果四叉树。

示例 2：

输入：quadTree1 = [[1,0]]
, quadTree2 = [[1,0]]
输出：[[1,0]]
解释：两个数所表示的矩阵大小都为 1*1，值全为 0 
结果矩阵大小为 1*1，值全为 0 。

示例 3：

输入：quadTree1 = [[0,0],[1,0],[1,0],[1,1],[1,1]]
, quadTree2 = [[0,0],[1,1],[1,1],[1,0],[1,1]]
输出：[[1,1]]

示例 4：

输入：quadTree1 = [[0,0],[1,1],[1,0],[1,1],[1,1]]
, quadTree2 = [[0,0],[1,1],[0,1],[1,1],[1,1],null,null,null,null,[1,1],[1,0],[1,0],[1,1]]
输出：[[0,0],[1,1],[0,1],[1,1],[1,1],null,null,null,null,[1,1],[1,0],[1,0],[1,1]]

示例 5：

输入：quadTree1 = [[0,1],[1,0],[0,1],[1,1],[1,0],null,null,null,null,[1,0],[1,0],[1,1],[1,1]]
, quadTree2 = [[0,1],[0,1],[1,0],[1,1],[1,0],[1,0],[1,0],[1,1],[1,1]]
输出：[[0,0],[0,1],[0,1],[1,1],[1,0],[1,0],[1,0],[1,1],[1,1],[1,0],[1,0],[1,1],[1,1]]

提示：

• quadTree1 和 quadTree2 都是符合题目要求的四叉树，每个都代表一个 n * n 的矩阵。
• n == 2^x ，其中 0 <= x <= 9.

思路

老长的题目，看的头痛

直接理解分析，一个四叉树分成四个区块，左上、右上、左下、右下

如果是 叶子节点，直接看val是否是1，是1就返回1，因为 1 || any = 1

val是0就返回any，怎么来的怎么返回

不是叶子节点，就去找四个区块，四个区块如果东西都相同，就返回1，不相同就递归返回四个区块向或的结果

代码

function intersect(quadTree1: Node | null, quadTree2: Node | null): Node | null {
    if (quadTree1.isLeaf) {
        if (quadTree1.val) {
            // 1 || any = 1
            return new Node(true,true)
        }
        // 0 || any = any
        return new Node(quadTree2.val, quadTree2.isLeaf, quadTree2.topLeft, quadTree2.topRight, quadTree2.bottomLeft, quadTree2.bottomRight)
    }
    if (quadTree2.isLeaf) {
        return intersect(quadTree2,quadTree1)
    }
    // 四个区块 或
    const r1 = intersect(quadTree1.topLeft, quadTree2.topLeft)
    const r2 = intersect(quadTree1.topRight, quadTree2.topRight)
    const r3 = intersect(quadTree1.bottomLeft, quadTree2.bottomLeft)
    const r4 = intersect(quadTree1.bottomRight, quadTree2.bottomRight)
    if (r1.isLeaf && r2.isLeaf && r3.isLeaf && r4.isLeaf && r1.val === r2.val && r1.val === r3.val && r1.val === r4.val) {
        return new Node(r1.val, true);
    }

    return new Node(false,false,r1,r2,r3,r4)
}

7.16 剑指 Offer II 041. 滑动窗口的平均值

题目

剑指 Offer II 041. 滑动窗口的平均值

给定一个整数数据流和一个窗口大小，根据该滑动窗口的大小，计算滑动窗口里所有数字的平均值。

实现 MovingAverage 类：

MovingAverage(int size) 用窗口大小 size 初始化对象。 double next(int val) 成员函数 next 每次调用的时候都会往滑动窗口增加一个整数，请计算并返回数据流中最后 size 个值的移动平均值，即滑动窗口里所有数字的平均值。

示例：

输入： inputs = ["MovingAverage", "next", "next", "next", "next"] inputs = [[3], [1], [10], [3], [5]] 输出： [null, 1.0, 5.5, 4.66667, 6.0]

解释： MovingAverage movingAverage = new MovingAverage(3); movingAverage.next(1); // 返回 1.0 = 1 / 1 movingAverage.next(10); // 返回 5.5 = (1 + 10) / 2 movingAverage.next(3); // 返回 4.66667 = (1 + 10 + 3) / 3 movingAverage.next(5); // 返回 6.0 = (10 + 3 + 5) / 3

提示：

1 <= size <= 1000 -105 <= val <= 105 最多调用 next 方法 104 次

来源：力扣（LeetCode） 链接：https://leetcode.cn/problems/qIsx9U 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

直接一个队列模拟即可

代码

class MovingAverage {
    arr: number[]
    size: number
    constructor(size: number) {
        this.arr = []
        this.size = size
    }

    next(val: number): number {
        let {arr, size} = this
        if (arr.length == size) {
            // 满了
            arr.shift()
            arr.push(val)
        } else {
            // 没满
            arr.push(val)
        }
        let res = 0
        arr.forEach(it => {res += it})
        return res / arr.length
    }
}

7.17 数组嵌套

题目

565. 数组嵌套

索引从0开始长度为N的数组A，包含0到N - 1的所有整数。找到最大的集合S并返回其大小，其中 S[i] = {A[i], A[A[i]], A[A[A[i]]], ... }且遵守以下的规则。

假设选择索引为i的元素A[i]为S的第一个元素，S的下一个元素应该是A[A[i]]，之后是A[A[A[i]]]... 以此类推，不断添加直到S出现重复的元素。

示例 1:

输入: A = [5,4,0,3,1,6,2]
输出: 4
解释: 
A[0] = 5, A[1] = 4, A[2] = 0, A[3] = 3, A[4] = 1, A[5] = 6, A[6] = 2.

其中一种最长的 S[K]:
S[0] = {A[0], A[5], A[6], A[2]} = {5, 6, 2, 0}

提示：

• 1 <= nums.length <= 105
• 0 <= nums[i] < nums.length
• A中不含有重复的元素。

思路

暴力肯定是过不了的（我也没试过），直接剪枝，将遍历过的数组元素置为-1，下次碰到直接跳过

代码

function arrayNesting(nums: number[]): number {
    let res = -1
    let len = nums.length
    for (let i = 0; i < len; i++) {
        if (nums[i] == -1) continue // 被标记过就跳过
        let t = nums[i]   // 新一轮的下标
        nums[i] = -1    // 遍历到的进行标记
        let tl = 1
        while (t != i) {
            tl++
            let tmp = nums[t]
            nums[t] = -1
            t = tmp
        }
        res = Math.max(tl,res)
    }
    return res
}

7.18 隔离病毒

题目

749. 隔离病毒

病毒扩散得很快，现在你的任务是尽可能地通过安装防火墙来隔离病毒。

假设世界由 m x n 的二维矩阵 isInfected 组成， isInfected[i][j] == 0 表示该区域未感染病毒，而 isInfected[i][j] == 1 表示该区域已感染病毒。可以在任意 2 个相邻单元之间的共享边界上安装一个防火墙（并且只有一个防火墙）。

每天晚上，病毒会从被感染区域向相邻未感染区域扩散，除非被防火墙隔离。现由于资源有限，每天你只能安装一系列防火墙来隔离其中一个被病毒感染的区域（一个区域或连续的一片区域），且该感染区域对未感染区域的威胁最大且 保证唯一 。

你需要努力使得最后有部分区域不被病毒感染，如果可以成功，那么返回需要使用的防火墙个数; 如果无法实现，则返回在世界被病毒全部感染时已安装的防火墙个数。

示例 1：

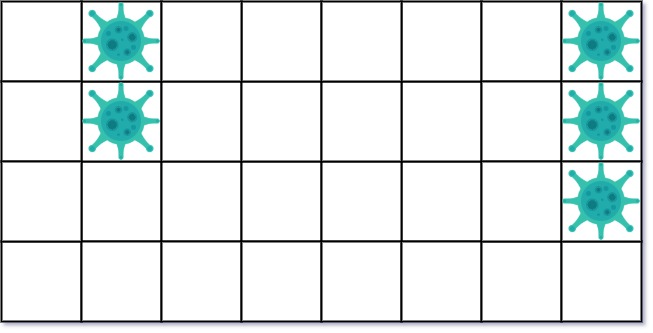
输入: isInfected = [[0,1,0,0,0,0,0,1],[0,1,0,0,0,0,0,1],[0,0,0,0,0,0,0,1],[0,0,0,0,0,0,0,0]]
输出: 10
解释:一共有两块被病毒感染的区域。
在第一天，添加 5 墙隔离病毒区域的左侧。病毒传播后的状态是:
第二天，在右侧添加 5 个墙来隔离病毒区域。此时病毒已经被完全控制住了。

示例 2：

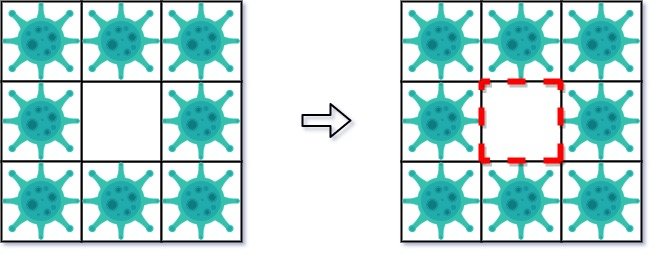
输入: isInfected = [[1,1,1],[1,0,1],[1,1,1]]
输出: 4
解释: 虽然只保存了一个小区域，但却有四面墙。
注意，防火墙只建立在两个不同区域的共享边界上。

示例 3:

输入: isInfected = [[1,1,1,0,0,0,0,0,0],[1,0,1,0,1,1,1,1,1],[1,1,1,0,0,0,0,0,0]]
输出: 13
解释: 在隔离右边感染区域后，隔离左边病毒区域只需要 2 个防火墙。

提示:

• m == isInfected.length
• n == isInfected[i].length
• 1 <= m, n <= 50
• isInfected[i][j] is either 0 or 1
• 在整个描述的过程中，总有一个相邻的病毒区域，它将在下一轮 严格地感染更多未受污染的方块

思路

纯纯的困难题。和感觉有点像迷宫了，只不过这个迷宫是动态的，里面的东西会变。

思路上直接dfs或者bfs我感觉都可以，但是我自己硬写就是写不出来，直接看题解，豁然贯通。

我这里就用bfs的思路，首先bfs一遍图，目的是找到威胁最大的病毒区域。每次扫一连串的病毒区域，假设一共有5堆不同的病毒，那就给这些病毒块每次遍历给上不同的数字。例如第一堆病毒给2，第二堆给3...以此类推。在遍历这5堆的过程中，记录每堆的病毒数量，最终病毒数量最多的那堆就是威胁最大的，同时也得到了威胁最大的病毒堆的数字

找完威胁最大的病毒堆之后，进行遍历整个图，如果遍历到的位置是该堆病毒，那就对其进行修补。修补完了给他一个特定的flag来标识其被修补了。修补一次记录加一次

最后对图中所有的未修补的病毒和即将感染病毒的区域进行重新赋值，让其变成1（也就是病毒），开始下一轮

所有的循环结束的条件就是，无法从图中找到当前最大威胁的病毒堆（全部都是病毒或者已经成功拦截）

代码

function containVirus(isInfected: number[][]): number {
    const m = isInfected.length
    const n = isInfected[0].length
    const dirs = [[0, 1], [1, 0], [-1, 0], [0, -1]] // 4个方向
    const FIX_FLAG = 2510 // 已经修复好的病毒区域的值（因为m，n最大50，最多是2500的病毒数量）

    const bfs = (i: number, j: number, num: number) => {
        // 是否遍历过的记忆数组
        let vis = new Array(m).fill(false).map(() => new Array(n).fill(false))
        let cnt = 0     // 即将感染的最大区域的数量
        vis[i][j] = true    // (i,j) 开始遍历
        let que: number[][] = []
        que.push([i, j])
        isInfected[i][j] = num  // 遍历过的点加入队列，并且将其置为num
        while (que.length) {
            let tmpQue: number[][] = []
            // 只要队列中还有点，就不会结束bfs
            for (const [i, j] of que) {
                // 遍历所有队列中的点
                for (const dir of dirs) {
                    // 遍历四个方向
                    const [x, y] = [i - dir[0], j - dir[1]]  // 周围4个的坐标
                    if (x < 0 || y < 0 || x >= m || y >= n) continue    // 保证不超出边界
                    if (isInfected[x][y] == 1) {
                        // 如果是病毒，放入临时队列中
                        tmpQue.push([x, y])
                        isInfected[x][y] = num  // 将其置为num
                    } else if (isInfected[x][y] <= 0) { // 等于0的地方是即将被感染的目前安全区，小于0的地方是已经被记录即将感染的区域
                        // 如果是即将被感染的区域
                        isInfected[x][y]--
                        if (!vis[x][y]) cnt++   // 每个即将感染的区域仅计数一次
                    }
                    vis[x][y] = true    // 遍历过的点，都给记录上
                }
            }
            que = tmpQue    // 新记录que，进行下一次循环
        }
        return cnt  // 返回最大区域的数量
    }

    const forEach = (fun: Function) => {
        for (let i = 0; i < m; i++) {
            for (let j = 0; j < n; j++) {
                fun(i, j)
            }
        }
    }

    let res = 0     // 最终封锁的次数

    while (true) {
        let startNum = 2    // zui
        let maxCnt = 0  // 病毒即将感染的区域数
        let finalNum = 1  // 威胁最大的那个病毒感染区域的数字

        // 找到最大的威胁病毒区域，将其数字变为startNum
        forEach((i: number, j: number) => {
            if (isInfected[i][j] == 1) {
                const cnt = bfs(i, j, startNum)
                if (cnt > maxCnt) {
                    maxCnt = cnt
                    finalNum = startNum
                }
                startNum++
            }
        })

        // console.log(isInfected.reduce((a, b) => a + '\n' + b.join(), ''))
        // console.log("\n")

        if (maxCnt == 0) break  // 直到某一轮病毒无法继续感染了，就结束（无法感染有两种情况——封锁住了 or 全寄了）



        // 将最大威胁的病毒区域给封锁
        forEach((i: number, j: number) => {
            if (isInfected[i][j] == finalNum) {
                // 找到了是最大威胁病毒的区域，标记一下，对其进行修补
                isInfected[i][j] = FIX_FLAG
                for (let dir of dirs) {
                    // 遍历四个方向
                    const [x, y] = [i - dir[0], j - dir[1]]  // 周围4个的坐标
                    if (x < 0 || y < 0 || x >= m || y >= n) continue
                    if (isInfected[x][y] < 0) {
                        isInfected[x][y]++  // 周围的区域恢复，因为已经被阻隔了
                        res++   // 这里res++不需要考虑边界之类的，因为在上面我们对一个病毒周围的格子都进行了-1的操作，这里如果是-2就要进行2次的修补
                    }
                }
            }
        })

        // console.log(isInfected.reduce((a, b) => a + '\n' + b.join(), ''))
        // console.log("\n")

        // 进行下一轮病毒感染
        forEach((i: number, j: number) => {
            if (isInfected[i][j] != 0 && isInfected[i][j] != FIX_FLAG) {
                isInfected[i][j] = 1    // 无论是已感染区域还是即将被感染的区域，在下一轮都是感染状态
            }
        })

        // console.log(isInfected.reduce((a, b) => a + '\n' + b.join(), ''))
        // console.log(res)

    }
    return res

}

7.19 我的日程安排表 II

题目

731. 我的日程安排表 II

实现一个 MyCalendar 类来存放你的日程安排。如果要添加的时间内不会导致三重预订时，则可以存储这个新的日程安排。

MyCalendar 有一个 book(int start, int end)方法。它意味着在 start 到 end 时间内增加一个日程安排，注意，这里的时间是半开区间，即 [start, end), 实数 x 的范围为， start <= x < end。

当三个日程安排有一些时间上的交叉时（例如三个日程安排都在同一时间内），就会产生三重预订。

每次调用 MyCalendar.book方法时，如果可以将日程安排成功添加到日历中而不会导致三重预订，返回 true。否则，返回 false 并且不要将该日程安排添加到日历中。

请按照以下步骤调用MyCalendar 类: MyCalendar cal = new MyCalendar(); MyCalendar.book(start, end)

示例：

MyCalendar();
MyCalendar.book(10, 20); // returns true
MyCalendar.book(50, 60); // returns true
MyCalendar.book(10, 40); // returns true
MyCalendar.book(5, 15); // returns false
MyCalendar.book(5, 10); // returns true
MyCalendar.book(25, 55); // returns true
解释： 
前两个日程安排可以添加至日历中。 第三个日程安排会导致双重预订，但可以添加至日历中。
第四个日程安排活动（5,15）不能添加至日历中，因为它会导致三重预订。
第五个日程安排（5,10）可以添加至日历中，因为它未使用已经双重预订的时间10。
第六个日程安排（25,55）可以添加至日历中，因为时间 [25,40] 将和第三个日程安排双重预订；
时间 [40,50] 将单独预订，时间 [50,55）将和第二个日程安排双重预订。

提示：

• 每个测试用例，调用 MyCalendar.book 函数最多不超过 1000次。
• 调用函数 MyCalendar.book(start, end)时， start 和 end 的取值范围为 [0, 10^9]。

思路

公交车算法，这里和7.5那里的算法思路是一样的，直接改一个公交车最大载荷人数为2就行了！

代码

class MyCalendarTwo {
    map: Map<number, number>
    constructor() {
        this.map = new Map()
    }

    book(start: number, end: number): boolean {
        let map = this.map
        map.set(start,  map.get(start) === undefined ? 1 : map.get(start) + 1)
        map.set(end, map.get(end) === undefined ? -1 : map.get(end) - 1)
        let arr = Array.from(map)
        arr.sort((a,b) => {return a[0] - b[0]})
        let tmp = 0
        for (let val of arr) {
            tmp += val[1]
            if (tmp > 2) {
                // 还原
                map.set(start, map.get(start) === undefined ? -1 : map.get(start) - 1)
                map.set(end, map.get(end) === undefined ? 1 : map.get(end) + 1)
                return false
            }
        }
        return true
    }
}

这里得提一嘴，时间复杂度高是因为每次book都sort了一遍map，如果是TreeMap，那直接会有顺序的，但是ts没有现成的TreeMap的组件，我也懒得手写，直接给map去sort一下

7.20 二维网格迁移

题目

1260. 二维网格迁移

给你一个 m 行 n 列的二维网格 grid 和一个整数 k。你需要将 grid 迁移 k 次。

每次「迁移」操作将会引发下述活动：

• 位于 grid[i][j] 的元素将会移动到 grid[i][j + 1]。
• 位于 grid[i][n - 1] 的元素将会移动到 grid[i + 1][0]。
• 位于 grid[m - 1][n - 1] 的元素将会移动到 grid[0][0]。

请你返回 k 次迁移操作后最终得到的 二维网格。

示例 1：

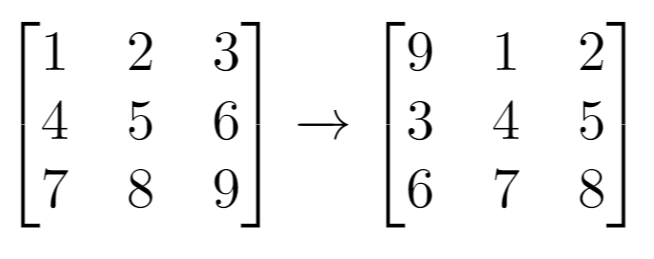
输入：grid = [[1,2,3],[4,5,6],[7,8,9]], k = 1
输出：[[9,1,2],[3,4,5],[6,7,8]]

示例 2：

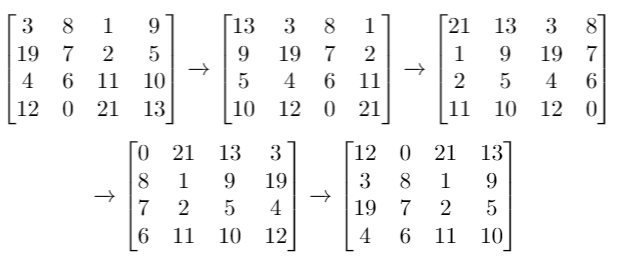
输入：grid = [[3,8,1,9],[19,7,2,5],[4,6,11,10],[12,0,21,13]], k = 4
输出：[[12,0,21,13],[3,8,1,9],[19,7,2,5],[4,6,11,10]]

示例 3：

输入：grid = [[1,2,3],[4,5,6],[7,8,9]], k = 9
输出：[[1,2,3],[4,5,6],[7,8,9]]

提示：

• m == grid.length
• n == grid[i].length
• 1 <= m <= 50
• 1 <= n <= 50
• -1000 <= grid[i][j] <= 1000
• 0 <= k <= 100

思路

直接模拟，暴力就完事了，简单题简单做

代码

function shiftGrid(grid: number[][], k: number): number[][] {
    let m = grid.length
    let n = grid[0].length
    if (k === m * n) {
        return grid
    }
    let res: number[][] = []
    for(let i = 0; i < m; i++){
        res.push(grid[i].concat())
    }
    for (let c = 0; c < k; c++) {
        if (c != 0) {
            grid = []
            for(let i = 0; i < m; i++){
                grid.push(res[i].concat())
            }
        }
        for (let i = 0; i < m; i++) {
            for (let j = 0; j < n; j++) {
                if (j === n-1) {
                    if (i === m-1) {
                        res[0][0] = grid[i][j]
                    } else {
                        res[i+1][0] = grid[i][j]
                    } 
                } else {
                    res[i][j+1] = grid[i][j]
                }
            }
        }
    }
    return res
}

7.21 二叉树剪枝

题目

814. 二叉树剪枝

给你二叉树的根结点 root ，此外树的每个结点的值要么是 0 ，要么是 1 。

返回移除了所有不包含 1 的子树的原二叉树。

节点 node 的子树为 node 本身加上所有 node 的后代。

示例 1：

输入：root = [1,null,0,0,1]
输出：[1,null,0,null,1]
解释：
只有红色节点满足条件“所有不包含 1 的子树”。 右图为返回的答案。

示例 2：

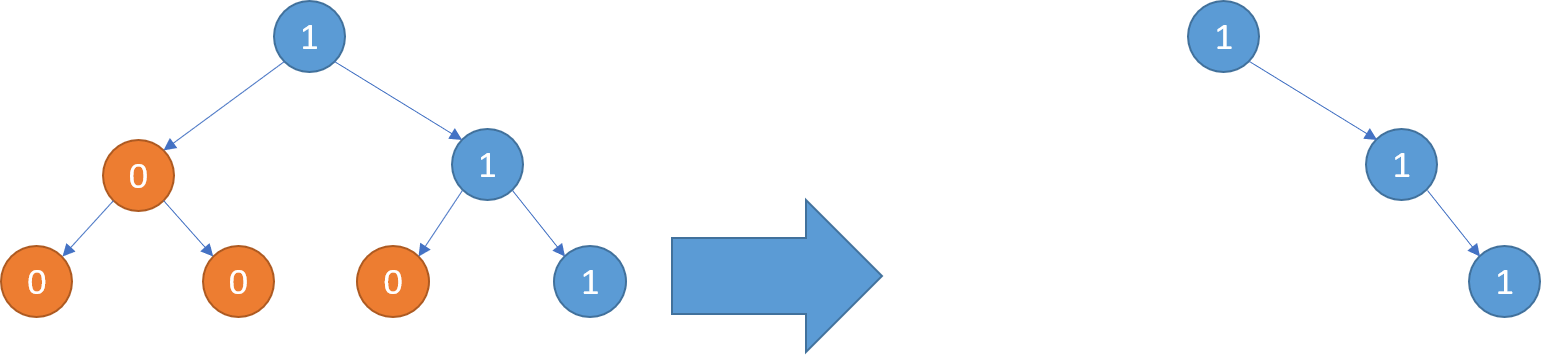
输入：root = [1,0,1,0,0,0,1]
输出：[1,null,1,null,1]

示例 3：

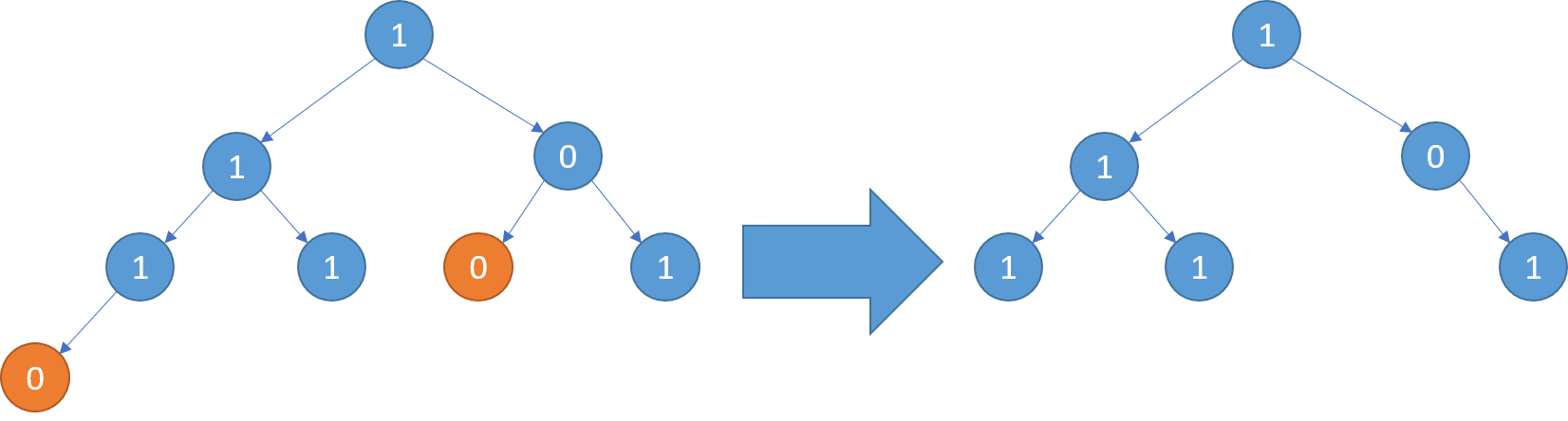
输入：root = [1,1,0,1,1,0,1,0]
输出：[1,1,0,1,1,null,1]

提示：

• 树中节点的数目在范围 [1, 200] 内
• Node.val 为 0 或 1

思路

对二叉树真的是又爱又恨。不过这题还是想得出来的，直接先中序遍历，遍历的过程中查看当前遍历到的节点是否是为0，如果是0，就去判断这个0节点的子孙是否有1，有1就保留，没有就置为null

就这么简单，代码直接递归就完事了，中序遍历一个递归，判断是否含有1也是一个递归

代码

function pruneTree(root: TreeNode | null): TreeNode | null {
    if (root == null) {
        return null
    }

    // 中序遍历
    const middleOrder = (root: TreeNode | null): TreeNode | null => {
        if (root == null || (root.val == 0 && !hasOne(root))) return null
        root.left = middleOrder(root.left)
        root.right = middleOrder(root.right)
        return root
    }

    // 判断这棵树是否有1
    const hasOne = (root: TreeNode | null): boolean => {
        if (root == null) return false
        if (root.val == 1) return true
        return  hasOne(root.left) || hasOne(root.right)
    }

    return middleOrder(root)
}

7.22 设置交集大小至少为2

题目

757. 设置交集大小至少为2

一个整数区间 [a, b] ( a < b ) 代表着从 a 到 b 的所有连续整数，包括 a 和 b。

给你一组整数区间intervals，请找到一个最小的集合 S，使得 S 里的元素与区间intervals中的每一个整数区间都至少有2个元素相交。

输出这个最小集合S的大小。

示例 1:

输入: intervals = [[1, 3], [1, 4], [2, 5], [3, 5]]
输出: 3
解释:
考虑集合 S = {2, 3, 4}. S与intervals中的四个区间都有至少2个相交的元素。
且这是S最小的情况，故我们输出3。

示例 2:

输入: intervals = [[1, 2], [2, 3], [2, 4], [4, 5]]
输出: 5
解释:
最小的集合S = {1, 2, 3, 4, 5}.

注意:

1. intervals 的长度范围为[1, 3000]。
2. intervals[i] 长度为 2，分别代表左、右边界。
3. intervals[i][j] 的值是 [0, 10^8]范围内的整数。

思路

直接贪心，首先按照右边界为基准，右边界相同的，按照左边界降序排序

然后遍历数组，有三种情况

• 两者没有交集
• 两者有一个交集
• 有多个交集

代码

function intersectionSizeTwo(intervals: number[][]): number {
    intervals.sort((a:number[],b:number[]) => {
        return a[1] == b[1] ?  b[0] - a[0] : a[1] - b[1]  
    })
    console.log(intervals)
    let res = [-1,-1]
    intervals.forEach(item => {
        let f = res.length - 2
        let s = f + 1
        if (item[0] <= res[f]) {
            return true
        }
        if (item[0] > res[s]) {
            res.push(item[1] - 1)
        }
        res.push(item[1])
    })
    console.log(res)
    return res.length - 2
}

7.23 剑指 Offer II 115. 重建序列

题目

剑指 Offer II 115. 重建序列

给定一个长度为 n 的整数数组 nums ，其中 nums 是范围为 [1，n] 的整数的排列。还提供了一个 2D 整数数组 sequences ，其中 sequences[i] 是 nums 的子序列。 检查 nums 是否是唯一的最短 超序列 。最短 超序列 是 长度最短 的序列，并且所有序列 sequences[i] 都是它的子序列。对于给定的数组 sequences ，可能存在多个有效的 超序列 。

例如，对于 sequences = [[1,2],[1,3]] ，有两个最短的 超序列 ，[1,2,3] 和 [1,3,2] 。 而对于 sequences = [[1,2],[1,3],[1,2,3]] ，唯一可能的最短 超序列 是 [1,2,3] 。[1,2,3,4] 是可能的超序列，但不是最短的。 如果 nums 是序列的唯一最短 超序列 ，则返回 true ，否则返回 false 。 子序列 是一个可以通过从另一个序列中删除一些元素或不删除任何元素，而不改变其余元素的顺序的序列。

示例 1：

输入：nums = [1,2,3], sequences = [[1,2],[1,3]] 输出：false 解释：有两种可能的超序列：[1,2,3]和[1,3,2]。 序列 [1,2] 是[1,2,3]和[1,3,2]的子序列。 序列 [1,3] 是[1,2,3]和[1,3,2]的子序列。 因为 nums 不是唯一最短的超序列，所以返回false。

示例 2：

输入：nums = [1,2,3], sequences = [[1,2]] 输出：false 解释：最短可能的超序列为 [1,2]。 序列 [1,2] 是它的子序列：[1,2]。 因为 nums 不是最短的超序列，所以返回false。

示例 3：

输入：nums = [1,2,3], sequences = [[1,2],[1,3],[2,3]] 输出：true 解释：最短可能的超序列为[1,2,3]。 序列 [1,2] 是它的一个子序列：[1,2,3]。 序列 [1,3] 是它的一个子序列：[1,2,3]。 序列 [2,3] 是它的一个子序列：[1,2,3]。 因为 nums 是唯一最短的超序列，所以返回true。

提示：

• n == nums.length
• 1 <= n <= 104
• nums 是 [1, n] 范围内所有整数的排列
• 1 <= sequences.length <= 104
• 1 <= sequences[i].length <= 104
• 1 <= sum(sequences[i].length) <= 105
• 1 <= sequences[i][j] <= n
• sequences 的所有数组都是 唯一 的
• sequences[i] 是 nums 的一个子序列

思路

拓扑排序，先对所有点进行入度计算

bfs对每次入度为0的节点加入队列，如果队列长度>1就false，同时对入度为0的节点的儿子们，进行题目的入度-1的操作，判断减完之后是否入度为0，是的话加入队列进行下一次bfs

最后判断入度是否有大于0的，有的话就有问题，都是0就是唯一最短超序列

代码

function sequenceReconstruction(nums: number[], sequences: number[][]): boolean {
    let len: number = nums.length
    let map: number[][] = new Array(len+1)  // map[i]表示i指向的儿子们
    for (let i = 0; i < map.length; i++) map[i] = new Array()
    let degree: number[] = new Array(len + 1).fill(0)
    degree[0] = -1  // degree[i]表示i的度数，nums是从1开始的，所以0没用

    // 存入map
    sequences.forEach(it => {
        for (let i = 1; i < it.length; i++) {
            map[it[i-1]].push(it[i])
            degree[it[i]]++
        }
    })

    // 拓扑排序
    let que: number[] = []
    degree.forEach((it, idx) => {if (it === 0) que.push(idx)}) // 入度为0的数字进入队列

    while (que.length) {
        if (que.length > 1) return false  // 如果有多个入度为0的点，那么就是无法推测唯一最短序列
        let idx: number = que.shift()
        let sons: number[] = map[idx]
        sons.forEach(it => {
            degree[it]-- // 所有的儿子，入度-1
            if (!degree[it]) que.push(it)  // 再次查找入度为0的节点
        })
    }

    return !degree.some((val) => val > 0)   // 如果存在入度大于0的，证明有问题
}

7.24 公交站间的距离

题目

1184. 公交站间的距离

环形公交路线上有 n 个站，按次序从 0 到 n - 1 进行编号。我们已知每一对相邻公交站之间的距离，distance[i] 表示编号为 i 的车站和编号为 (i + 1) % n 的车站之间的距离。

环线上的公交车都可以按顺时针和逆时针的方向行驶。

返回乘客从出发点 start 到目的地 destination 之间的最短距离。

示例 1：

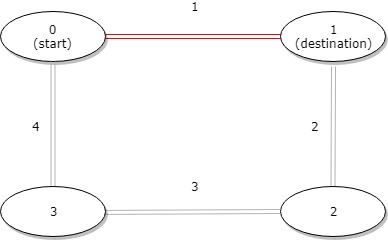
输入：distance = [1,2,3,4], start = 0, destination = 1
输出：1
解释：公交站 0 和 1 之间的距离是 1 或 9，最小值是 1。

示例 2：

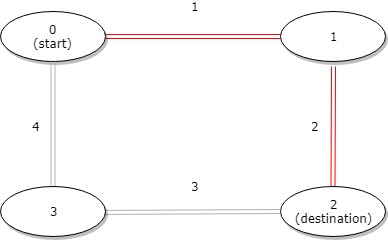
输入：distance = [1,2,3,4], start = 0, destination = 2
输出：3
解释：公交站 0 和 2 之间的距离是 3 或 7，最小值是 3。

示例 3：

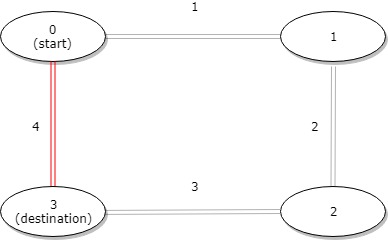
输入：distance = [1,2,3,4], start = 0, destination = 3
输出：4
解释：公交站 0 和 3 之间的距离是 6 或 4，最小值是 4。

提示：

• 1 <= n <= 10^4
• distance.length == n
• 0 <= start, destination < n
• 0 <= distance[i] <= 10^4

思路

简单题，模拟即可，需要注意边界，我这里用取模处理

代码

function distanceBetweenBusStops(distance: number[], start: number, destination: number): number {

    if (start > destination) {
        let tmp = start
        start = destination
        destination = tmp
    }

    const res1 = () => {
        let res = 0;
        for (let i = start; i < destination; i++) {
            res += distance[i]
        }
        return res
    }

    const res2  = () => {
        let res = 0
        for (let i = destination; i != start; i = (i + 1) % distance.length) {
            res += distance[i]
        }
        return res
    }

    return Math.min(res1(),res2())
}

7.25 完全二叉树插入器

题目

919. 完全二叉树插入器

完全二叉树 是每一层（除最后一层外）都是完全填充（即，节点数达到最大）的，并且所有的节点都尽可能地集中在左侧。

设计一种算法，将一个新节点插入到一个完整的二叉树中，并在插入后保持其完整。

实现 CBTInserter 类:

• CBTInserter(TreeNode root) 使用头节点为 root 的给定树初始化该数据结构；
• CBTInserter.insert(int v) 向树中插入一个值为 Node.val == val的新节点 TreeNode。使树保持完全二叉树的状态，并返回插入节点 TreeNode 的父节点的值；
• CBTInserter.get_root() 将返回树的头节点。

示例 1：

输入
["CBTInserter", "insert", "insert", "get_root"]
[[[1, 2]], [3], [4], []]
输出
[null, 1, 2, [1, 2, 3, 4]]

解释
CBTInserter cBTInserter = new CBTInserter([1, 2]);
cBTInserter.insert(3);  // 返回 1
cBTInserter.insert(4);  // 返回 2
cBTInserter.get_root(); // 返回 [1, 2, 3, 4]

提示：

• 树中节点数量范围为 [1, 1000]
• 0 <= Node.val <= 5000
• root 是完全二叉树
• 0 <= val <= 5000
• 每个测试用例最多调用 insert 和 get_root 操作 104 次

思路

层序遍历，看看这一层还有没有空位，有就直接插，没有就去下一层

直接队列遍历每层

代码

class CBTInserter {
    tree: TreeNode
    constructor(root: TreeNode | null) {
        this.tree = root as TreeNode
    }

    insert(val: number): number {
        let res = 0
        let root = this.tree
         // 层序遍历
        let arr = []
        arr.push(root)
        while (arr.length !== 0) {
            let len = arr.length
            for (let i = 0; i < len; i++) {
                let tmp = arr.shift()   // 队头
                // 左空，插入左边
                if (tmp.left === null) {
                    tmp.left = new TreeNode(val)
                    return tmp.val
                }
                // 插不了左，就插右
                if (tmp.right === null) {
                   tmp.right = new TreeNode(val)
                   return tmp.val
                }
                // 左树不空
                if (tmp.left !== null) arr.push(tmp.left)
                // 右树不空
                if (tmp.right !== null) arr.push(tmp.right)
            }
        }
        return res
    }

    get_root(): TreeNode | null {
        return this.tree
    }
}

7.26 设计跳表

题目

1206. 设计跳表

跳表 是在 O(log(n)) 时间内完成增加、删除、搜索操作的数据结构。跳表相比于树堆与红黑树，其功能与性能相当，并且跳表的代码长度相较下更短，其设计思想与链表相似。

例如，一个跳表包含 [30, 40, 50, 60, 70, 90] ，然后增加 80、45 到跳表中，以下图的方式操作：

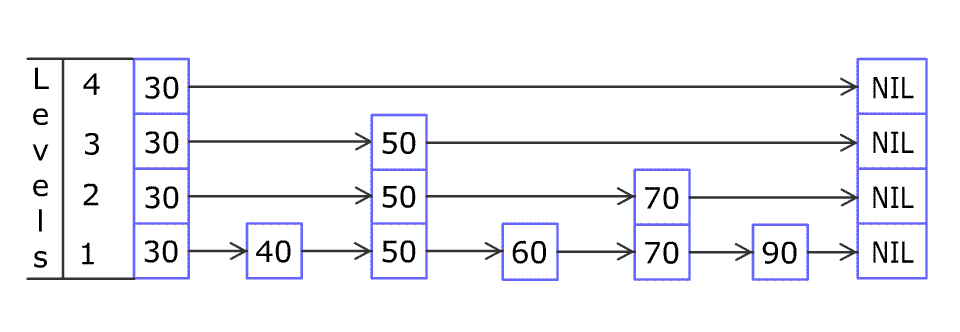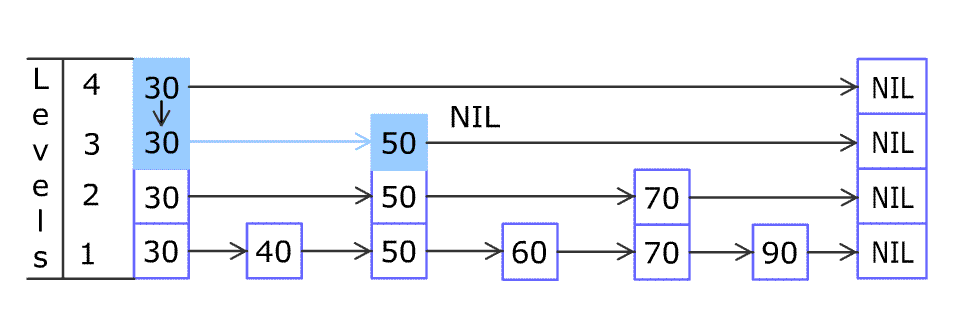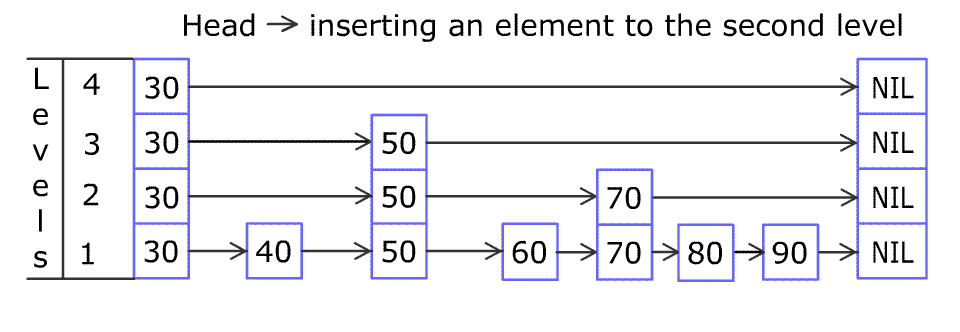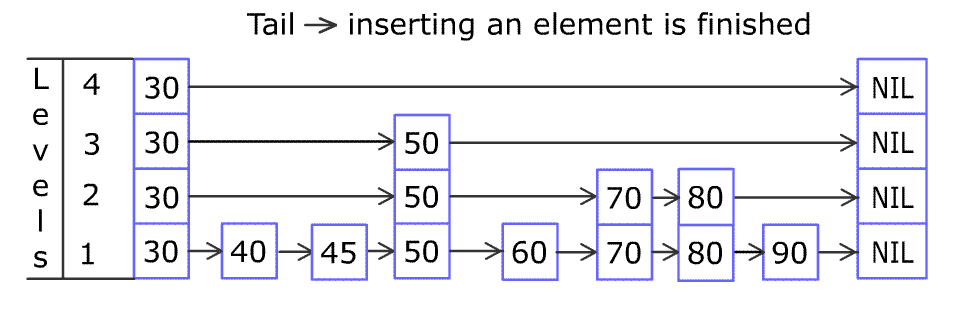Artyom Kalinin [CC BY-SA 3.0], via Wikimedia Commons

跳表中有很多层，每一层是一个短的链表。在第一层的作用下，增加、删除和搜索操作的时间复杂度不超过 O(n)。跳表的每一个操作的平均时间复杂度是 O(log(n))，空间复杂度是 O(n)。

了解更多 : https://en.wikipedia.org/wiki/Skip_list

在本题中，你的设计应该要包含这些函数：

• bool search(int target) : 返回target是否存在于跳表中。
• void add(int num): 插入一个元素到跳表。
• bool erase(int num): 在跳表中删除一个值，如果 num 不存在，直接返回false. 如果存在多个 num ，删除其中任意一个即可。

注意，跳表中可能存在多个相同的值，你的代码需要处理这种情况。

示例 1:

输入
["Skiplist", "add", "add", "add", "search", "add", "search", "erase", "erase", "search"]
[[], [1], [2], [3], [0], [4], [1], [0], [1], [1]]
输出
[null, null, null, null, false, null, true, false, true, false]

解释
Skiplist skiplist = new Skiplist();
skiplist.add(1);
skiplist.add(2);
skiplist.add(3);
skiplist.search(0);   // 返回 false
skiplist.add(4);
skiplist.search(1);   // 返回 true
skiplist.erase(0);    // 返回 false，0 不在跳表中
skiplist.erase(1);    // 返回 true
skiplist.search(1);   // 返回 false，1 已被擦除

提示:

• 0 <= num, target <= 2 * 104
• 调用search, add, erase操作次数不大于 5 * 104

思路

一个不需要脑子的方法就是卡题目限制，直接一个20001长度的数组就能做到基础功能

但还是需要学学如何手撕调表这个数据结构，建议直接看题解，反正我是不会实现（汗

代码

投机取巧版：

class Skiplist {
    list: Array<number>
    constructor() {
        this.list = new Array<number>(20001)
        this.list.fill(0)
    }

    search(target: number): boolean {
        return this.list[target] > 0
    }

    add(num: number): void {
        this.list[num]++
    }

    erase(num: number): boolean {
        if (this.list[num] === 0) return false
        this.list[num]--
        return true
    }
}

跳表：

const MAX_LEVEL = 32
const SKIPLIST_P = 0.25
class Skiplist {
    head: SkipNode
    curLevel: number
    constructor() {
        this.head = new SkipNode(-1, MAX_LEVEL)
        this.curLevel = 0
    }

    search(target: number): boolean {
        let cur = this.head
        for (let i = this.curLevel - 1; i >= 0; i--) {
            while (cur.next[i] != undefined && cur.next[i].val < target) {
                cur = cur.next[i]
            }
        }
        cur = cur.next[0]
        return cur != undefined && cur.val == target
    }

    add(num: number): void {
        let updates = new Array<SkipNode>(MAX_LEVEL).fill(this.head)
        let cur = this.head
        for (let i = this.curLevel - 1; i >= 0; i--) {
            while (cur.next[i] != undefined && cur.next[i].val < num) {
                cur = cur.next[i]
            }
            updates[i] = cur
        }
        let level = 1
        while (Math.random() < SKIPLIST_P && level < MAX_LEVEL) {
            level++
        }
        this.curLevel = Math.max(this.curLevel, level)
        let newNode = new SkipNode(num, level)
        for (let i =0; i < level; i++) {
            newNode.next[i] = updates[i].next[i]
            updates[i].next[i] = newNode
        }
    }

    erase(num: number): boolean {
        let updates = new Array<SkipNode>(MAX_LEVEL)
        let cur = this.head
        for (let i = this.curLevel - 1; i >= 0; i--) {
            while (cur.next[i] != undefined && cur.next[i].val < num) {
                cur = cur.next[i]
            }
            updates[i] = cur
        }
        cur = cur.next[0]
        if (cur == undefined || cur.val != num) {
            return false
        }
        for (let i = 0; i < this.curLevel; i++) {
            if (updates[i].next[i] != cur) {
                break
            }
            updates[i].next[i] = cur.next[i]
        }
        while (this.curLevel > 1 && this.head.next[this.curLevel - 1] == undefined) {
            this.curLevel--
        } 
        return true
    }
}

class SkipNode {
    next: SkipNode[]
    val: number
    constructor(val: number, len: number) {
        this.val = val
        this.next = new Array(len)
    }
}

20001数组的比这个跳表还快，omg

7.27 分数加减运算

题目

592. 分数加减运算

给定一个表示分数加减运算的字符串 expression ，你需要返回一个字符串形式的计算结果。

这个结果应该是不可约分的分数，即最简分数。 如果最终结果是一个整数，例如 2，你需要将它转换成分数形式，其分母为 1。所以在上述例子中, 2 应该被转换为 2/1。

示例 1:

输入: expression = "-1/2+1/2"
输出: "0/1"

示例 2:

输入: expression = "-1/2+1/2+1/3"
输出: "1/3"

示例 3:

输入: expression = "1/3-1/2"
输出: "-1/6"

提示:

• 输入和输出字符串只包含 '0' 到 '9' 的数字，以及 '/', '+' 和 '-'。
• 输入和输出分数格式均为 ±分子/分母。如果输入的第一个分数或者输出的分数是正数，则 '+' 会被省略掉。
• 输入只包含合法的最简分数，每个分数的分子与分母的范围是 [1,10]。 如果分母是1，意味着这个分数实际上是一个整数。
• 输入的分数个数范围是 [1,10]。
• 最终结果的分子与分母保证是 32 位整数范围内的有效整数。

思路

典型的输入数据处理，直接模拟就行了

我这里直接使用笨方法，先找到第一个分式，再找剩下的分式进行加减

代码

function fractionAddition(expression: string): string {
    let son: number = 0
    let mother: number = 0
    let sign: number = expression[0] === '-' ? -1 : 1
    let start: number = (sign === 1 ? 0 : 1) - 1
    let flagOfIsSon: boolean = true    // 现在转化的是否是分子
    // 先找到第一个分数
    while(start !== expression.length) {
        start++
        let char: string = expression[start]
        if (char >= '0' && char <= '9') {
            let tmpNum: number = parseInt(char)
            // 如果是数字
            if (flagOfIsSon) {
                // 分子
            son = son * 10 + tmpNum
            } else {
                // 分母
                mother = mother * 10 + tmpNum
            }
            continue
        }
        if (char === '/') {
            flagOfIsSon = false
            continue
        }
        if (char === '+' || char === '-') {
            flagOfIsSon = true
            break
        }
    }
    if (start === expression.length) return (sign === 1 ? "" : "-") + son + "/" + mother
    // 下一个分数的分子分母和前缀
    son = son * sign
    let nextSon: number = 0
    let nextMother: number = 0
    let nextSign: number = expression[start] === '+' ? 1 : -1
    // 如果还有多个分数，那么进行加减
    for (let i = start + 1; i < expression.length; i++) {
        let char: string = expression[i]
        // 符号
        if (char === '+' || char === '-') {
            // 处理计算加减
            son = (son * nextMother) + (nextSon * mother * nextSign)
            mother = mother * nextMother
            // 恢复现场
            flagOfIsSon = true
            nextSign = char === '+' ? 1 : -1
            nextSon = 0
            nextMother = 0
            continue
        }
        // 数字
        if (char >= '0' && char <= '9') {
            let tmpNum: number = parseInt(char)
            if (flagOfIsSon) nextSon = nextSon * 10 + tmpNum
            else nextMother = nextMother * 10 + tmpNum
            continue
        }
        // 分号
        if (char === '/') {
            flagOfIsSon = false
            continue
        }
    }
    // 出来最后计算一次加减
    son = (son * nextMother) + (nextSon * mother * nextSign)
    mother = mother * nextMother
    let gcdN = gcd(son,mother)
    if (son === 0) return "0/1"
    return (son / gcdN) + "/" + (mother / gcdN)
}

// 最大公约数
const gcd = (a: number, b: number): number => {
    if (a < 0) a = -a
    if (b < 0) b = -b
    if (b > a) { // 排序 让较大的数在前面
        let temp = a;
        a = b;
        b = temp;
    }
    if (a == b || b == 0) { 
        return a;
    }
    return gcd(b, a % b);
}

7.28 数组序号转换

题目

1331. 数组序号转换

给你一个整数数组 arr ，请你将数组中的每个元素替换为它们排序后的序号。

序号代表了一个元素有多大。序号编号的规则如下：

• 序号从 1 开始编号。
• 一个元素越大，那么序号越大。如果两个元素相等，那么它们的序号相同。
• 每个数字的序号都应该尽可能地小。

示例 1：

输入：arr = [40,10,20,30]
输出：[4,1,2,3]
解释：40 是最大的元素。 10 是最小的元素。 20 是第二小的数字。 30 是第三小的数字。

示例 2：

输入：arr = [100,100,100]
输出：[1,1,1]
解释：所有元素有相同的序号。

示例 3：

输入：arr = [37,12,28,9,100,56,80,5,12]
输出：[5,3,4,2,8,6,7,1,3]

思路

直接模拟，先复制一份list从小到大排序，再搞一个哈希表，记录值对应的下标

最后遍历一遍原数组，数值对应的下标就出来了

代码

function arrayRankTransform(arr: number[]): number[] {
    let clone = []
    Object.assign(clone, arr)
    clone.sort((a,b) => {return a-b})
    let n = arr.length, idx = 0
    let map = new Map<number, number>()
    for (const i of clone) 
        if (!map.has(i)) map.set(i, ++idx)
    let res = []
    for (let i = 0; i < n; i++)
        res.push(map.get(arr[i]))
    return res
}

7.29 有效的正方形

题目

593. 有效的正方形

给定2D空间中四个点的坐标 p1, p2, p3 和 p4，如果这四个点构成一个正方形，则返回 true 。

点的坐标 pi 表示为 [xi, yi] 。 输入没有任何顺序 。

一个 有效的正方形 有四条等边和四个等角(90度角)。

示例 1:

输入: p1 = [0,0], p2 = [1,1], p3 = [1,0], p4 = [0,1]
输出: True

示例 2:

输入：p1 = [0,0], p2 = [1,1], p3 = [1,0], p4 = [0,12]
输出：false

示例 3:

输入：p1 = [1,0], p2 = [-1,0], p3 = [0,1], p4 = [0,-1]
输出：true

提示:

• p1.length == p2.length == p3.length == p4.length == 2
• -104 <= xi, yi <= 104

思路

正方形拆成多个等腰直角三角形，数理证明即可

代码

贴一个题解区的版本，我写的又臭又长太丑了

let len = -1
function validSquare(a: number[], b: number[], c: number[], d: number[]): boolean {
    len = -1
    return calc(a, b, c) && calc(a, b, d) && calc(a, c, d) && calc(b, c, d)
};
function calc(a: number[], b: number[], c: number[]): boolean {
    const l1 = (a[0] - b[0]) * (a[0] - b[0]) + (a[1] - b[1]) * (a[1] - b[1])
    const l2 = (a[0] - c[0]) * (a[0] - c[0]) + (a[1] - c[1]) * (a[1] - c[1])
    const l3 = (b[0] - c[0]) * (b[0] - c[0]) + (b[1] - c[1]) * (b[1] - c[1])
    const ok = (l1 == l2 && l1 + l2 == l3) || (l1 == l3 && l1 + l3 == l2) || (l2 == l3 && l2 + l3 == l1)
    if (!ok) return false
    if (len == -1) len = Math.min(l1, l2)
    else if (len == 0 || len != Math.min(l1, l2)) return false
    return true
}

7.30 按公因数计算最大组件大小

题目

952. 按公因数计算最大组件大小

给定一个由不同正整数的组成的非空数组 nums ，考虑下面的图：

• 有 nums.length 个节点，按从 nums[0] 到 nums[nums.length - 1] 标记；
• 只有当 nums[i] 和 nums[j] 共用一个大于 1 的公因数时，nums[i] 和 nums[j]之间才有一条边。

返回 图中最大连通组件的大小 。

示例 1：

输入：nums = [4,6,15,35]
输出：4

示例 2：

输入：nums = [20,50,9,63]
输出：2

示例 3：

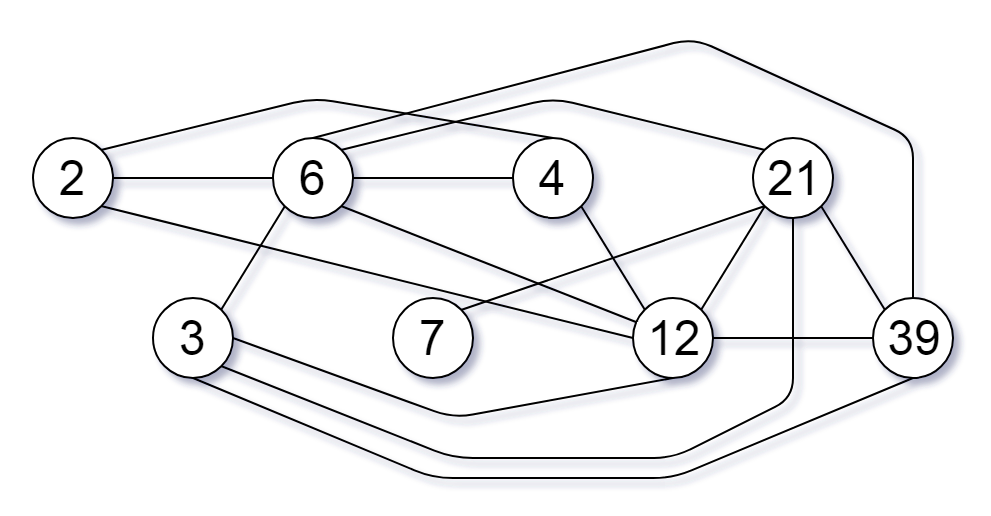
输入：nums = [2,3,6,7,4,12,21,39]
输出：8

提示：

• 1 <= nums.length <= 2 * 104
• 1 <= nums[i] <= 105
• nums 中所有值都 不同

思路

欧拉筛+并查集

代码

const N = 1e5 + 1
const parents = new Array(N).fill(0)
const isPrime = new Array(N).fill(0)
const primes = new Array(N).fill(0)
const union = (a: number, b: number) => {
    let pa = find(a)
    let pb = find(b)
    if (pa != pb) {
        parents[pa] = pb
    }
}
const find = (a: number) => {
    return parents[a] === a ? a : (parents[a] = find(parents[a]))
}
function largestComponentSize(nums: number[]): number {
    let k = 0
    //欧拉筛，找出1到n的所有质数
    for (let i = 2; i < N; i++) {
        if (isPrime[i] == 0) {
            primes[k++] = i;
        }
        for (let j = 0; primes[j] * i < N; j++) {
            isPrime[primes[j] * i] = 1;
            if (i % primes[j] == 0) {
                break;
            }
        }
    }
    //初始化并查集
    for (let i = 0; i < N; i++) {
        parents[i] = i;
    }
    //遍历nums中的每个数,和他们的质因数连接
    for (let num of nums) {
        let quotient = num;
        for (let j = 0; j < k && primes[j] * primes[j] <= quotient; j++) {
            if (quotient % primes[j] == 0) {
                //primes[i]是他的质因数
                union(num, primes[j]);
                while (quotient % primes[j] == 0) {
                    quotient /= primes[j];
                }
            }
        }
        if (quotient > 1) {
            union(quotient, num);
        }
    }
    let res = 0
    const cnt = new Array(N).fill(0)
    nums.forEach(it => {res = Math.max(res, ++cnt[find(it)])})
    return res
}

7.31 最大层内元素和

题目

1161. 最大层内元素和

给你一个二叉树的根节点 root。设根节点位于二叉树的第 1 层，而根节点的子节点位于第 2 层，依此类推。

请返回层内元素之和 最大 的那几层（可能只有一层）的层号，并返回其中 最小 的那个。

示例 1：

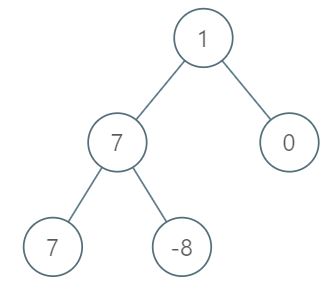
输入：root = [1,7,0,7,-8,null,null]
输出：2
解释：
第 1 层各元素之和为 1，
第 2 层各元素之和为 7 + 0 = 7，
第 3 层各元素之和为 7 + -8 = -1，
所以我们返回第 2 层的层号，它的层内元素之和最大。

示例 2：

输入：root = [989,null,10250,98693,-89388,null,null,null,-32127]
输出：2

提示：

• 树中的节点数在 [1, 104]范围内
• -105 <= Node.val <= 105

思路

直接层序遍历，每层记录sum，判断是否大于上一次记录的max

代码

function maxLevelSum(root: TreeNode | null): number {
    let arr = []
    let cnt = 1
    let res = 0
    let max = -Number.MAX_VALUE
    arr.push(root)
    while (arr.length != 0) {
        let curLen = arr.length
        let curSum = 0
        for (let i = 0; i < curLen; i++) {
            let tmpRoot = arr.shift()
            curSum += tmpRoot.val
            if (tmpRoot.left != null) {
                arr.push(tmpRoot.left)
            }
            if (tmpRoot.right != null) {
                arr.push(tmpRoot.right)
            }
        }
        if (curSum > max) {
            max = curSum
            res = cnt
        }
        cnt++
    }
    return res
}

后话

每日一题有些简单，有些难，还是感觉难点好，可以多学学数据结构和一些常用算法。这一个月刷完，印象最深的简单数据结构还是队列的使用，然后就是一些贪心算法（公交车）、bfs、dfs之类的，其次就是一些比较牛逼的数据结构（跳表、并查集）。