【离散数学】期末不挂科复习笔记
离散上的人散架了,不过里面的计算机相关知识还是得略懂一二的...
【离散数学】期末不挂科复习笔记
和蜂考学的,重要的应该是逻辑和函数这两大板块,图和树就与数据结构挂钩了(大部分都是之前学过的),重点看看各种逻辑的等值演算还有推理!
第一章(命题逻辑的基本概念)
1、命题的概念

如何判断是否是命题:

例题1:

2、命题连接词
①否定(可以理解为非)
②合取(可以理解成交)
③析取(可以理解为并)
④蕴含(可以理解为非p并q)
⑤等价(可以理解为相等)
优先级:

例题1:


3、命题公式及其赋值

成真赋值就是让p蕴含q的值为1,这种情况下p和q的赋值
成假赋值就是让p蕴含q的值为0,这种情况下p和q的赋值
例题1:
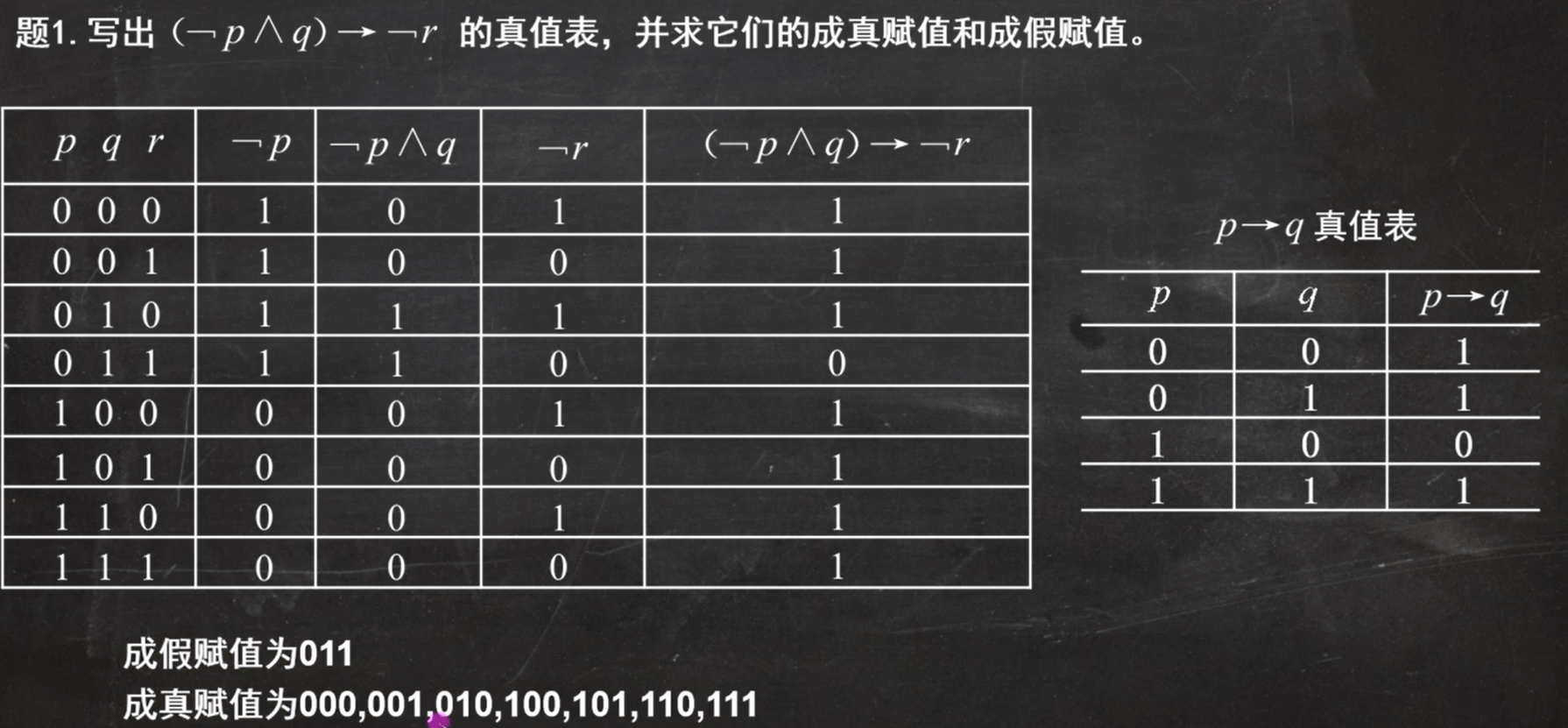
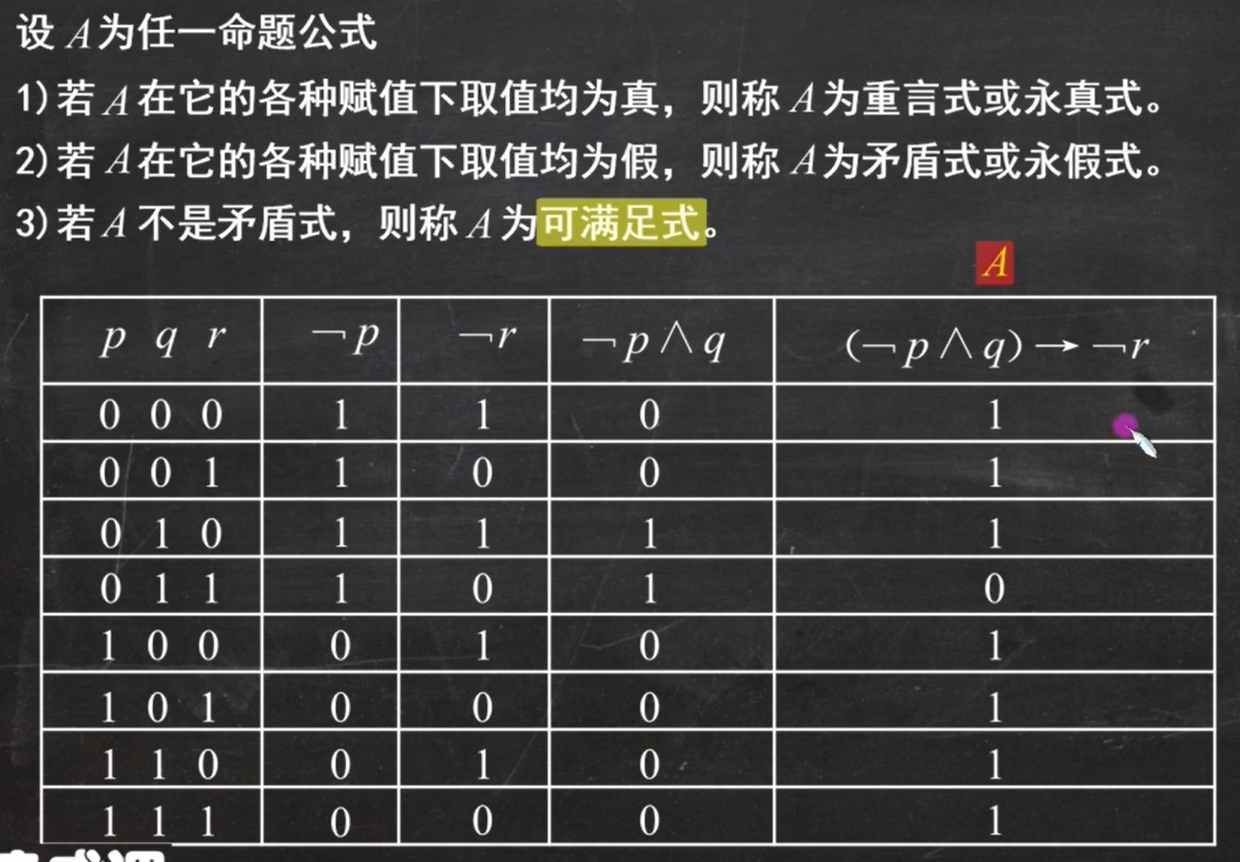
我们可以看出图上的式子是可满足式**(注意永真式也是可满足式)**
第二章(命题逻辑等值演算)
1、等值式

常见等值式:(结合数字电路知识点学习~)
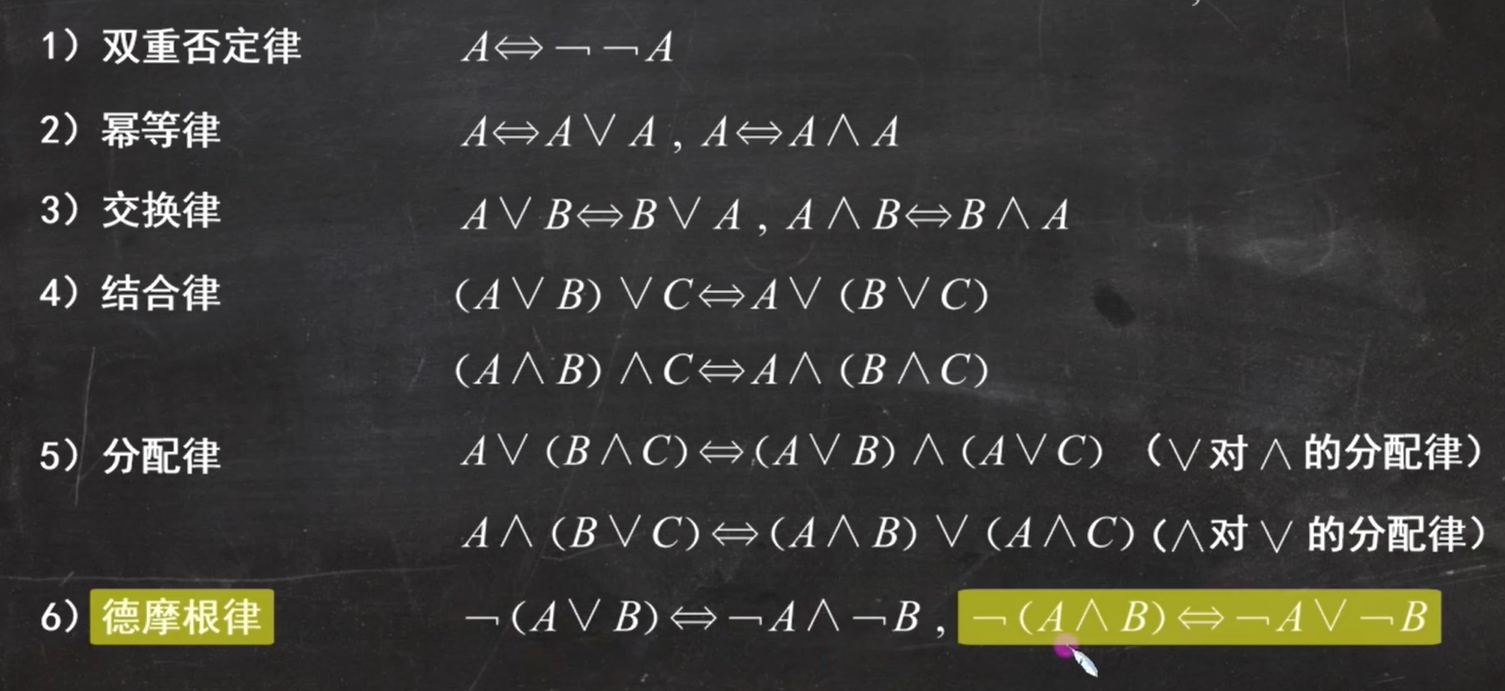
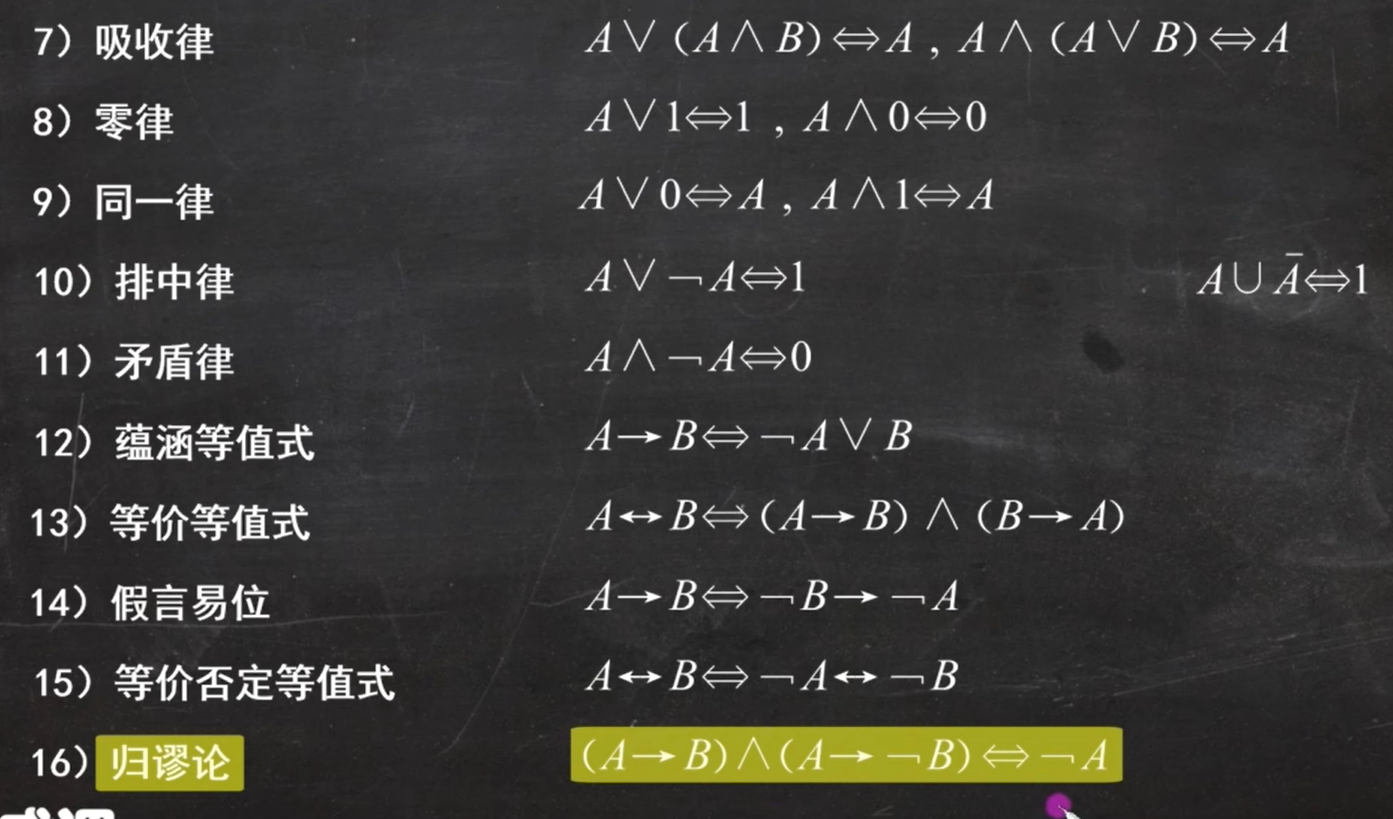
重点是(12),蕴含等值式
例题1:

例题2:

需要注意的是,用等值演算不能直接证明两个公式不等值
例题3:(证明两个公式不等值)

2、析取范式与合取范式

例题1:

例题2:

3、主析取范式与主合取范式
极小项与极大项的概念:


第一张表:
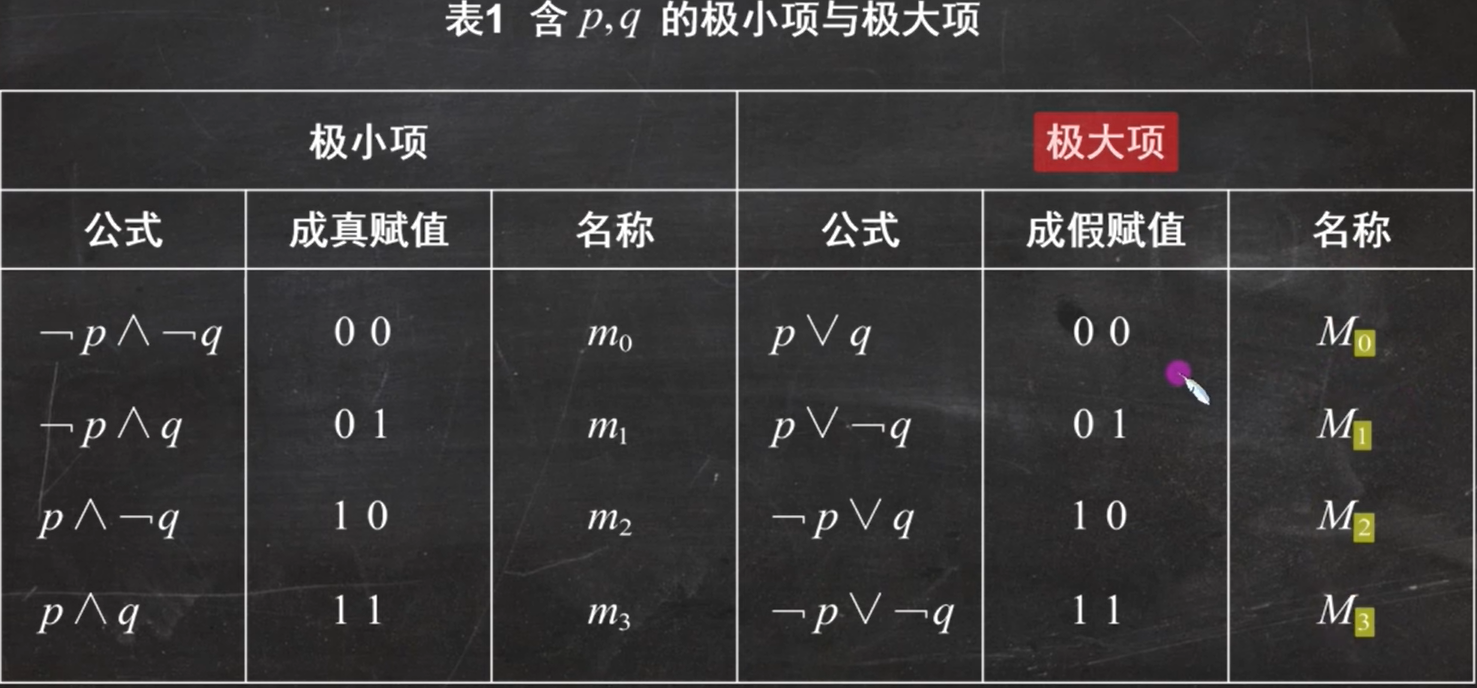
那么什么是主析取范式和主合取范式呢?


例题1:
这里使用的是真值表法
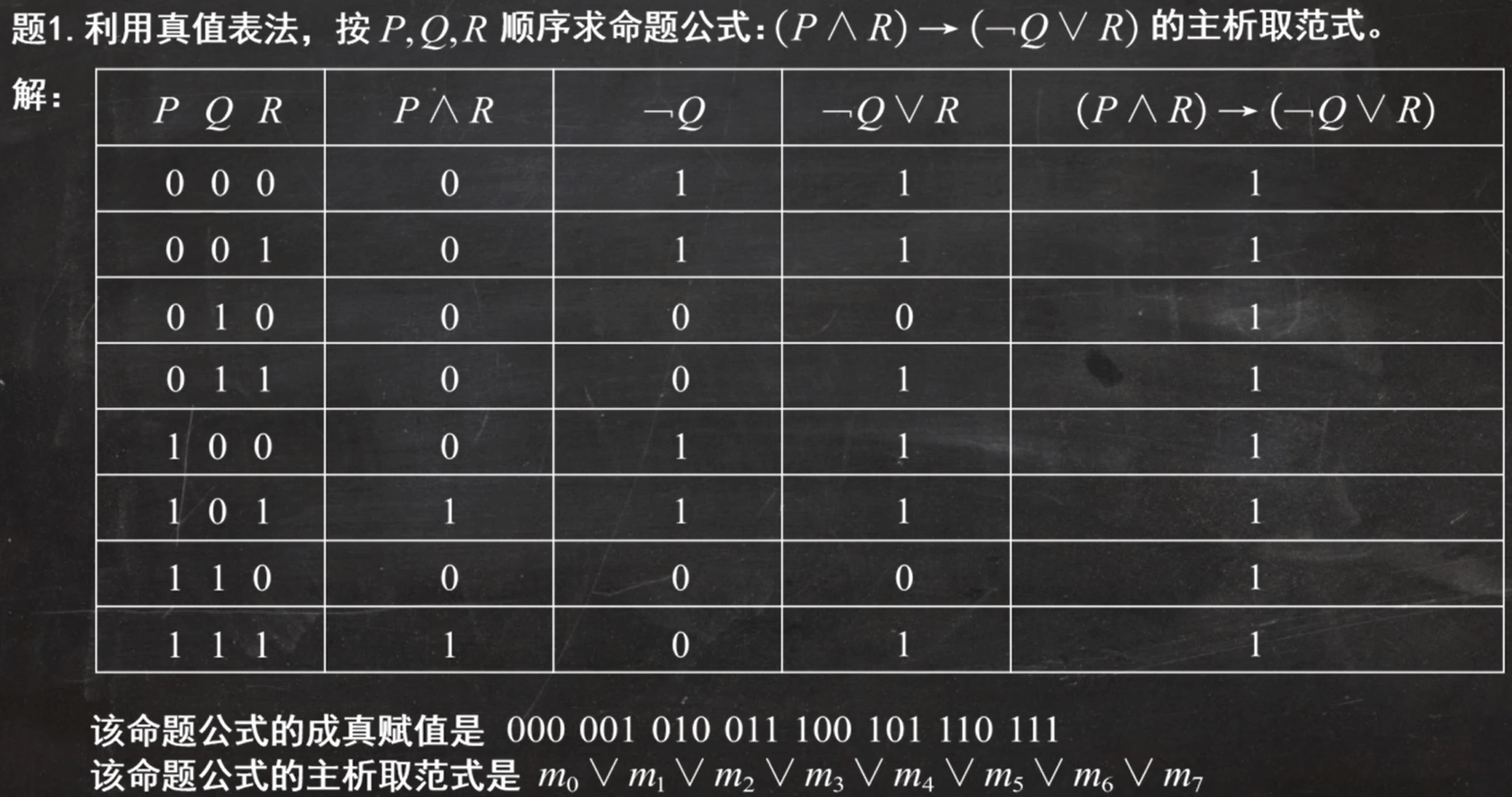
例题2:
引入一个前提:


例题3:
这里使用等值演算法

4、联结词的完备集


最小的联结词完备集就是图上的S4和S5,一定要有非
例题:

第三章(命题逻辑的推理理论)
1、推理的相关公式
推理定义:单项箭头(双向就是等值式了)
明确一点,放在左边的是前提,放在右边的是结论

判断推理正确

推理形式

非常多的推理公式(推理题型的基础)
标黄的是重点
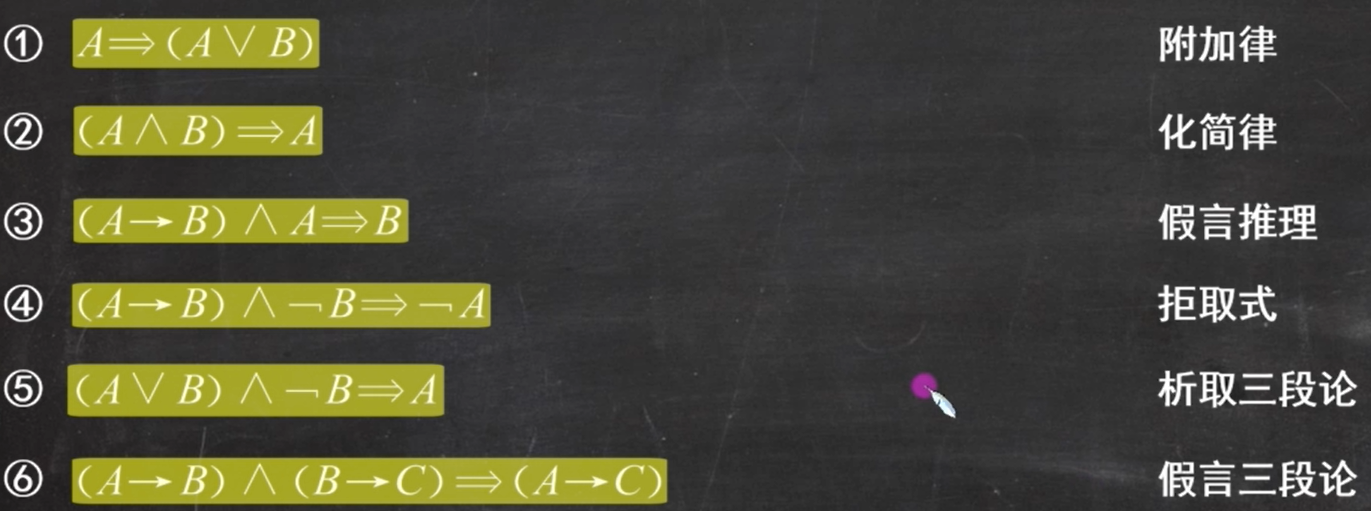
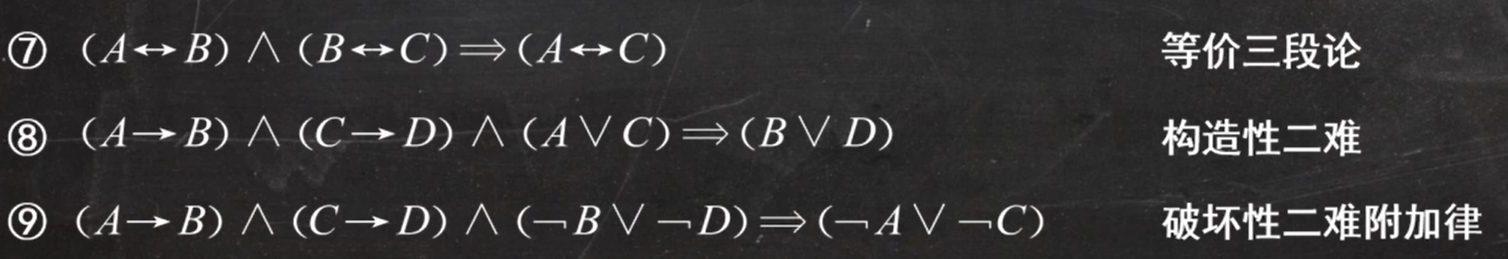
例题1:

例题2:
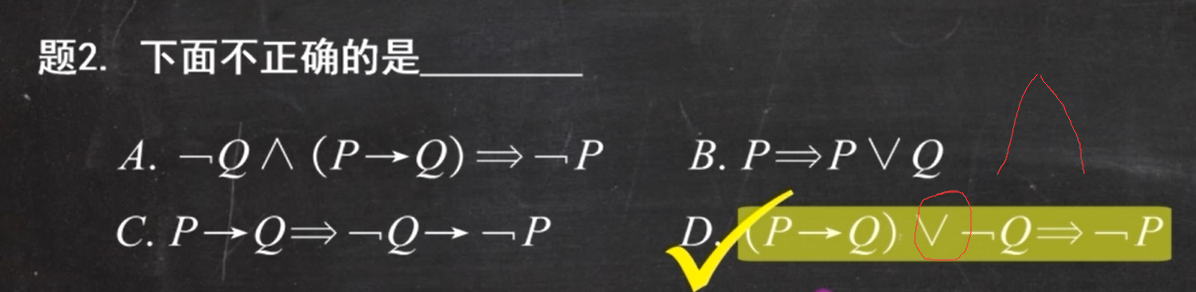
2、自然推理系统P
例题1:


例题2:

例题3:
附加前提法

例题4:
这里使用了归谬法,可以多引入一个否定的结论

第四章(谓词逻辑基本概念)
1、谓词逻辑命题符号化
谓词逻辑命题符号化的三个基本要素:个体词、谓词、量词(任意、存在)
例题1:
考察谓词

例题2、例题3:
考察量词
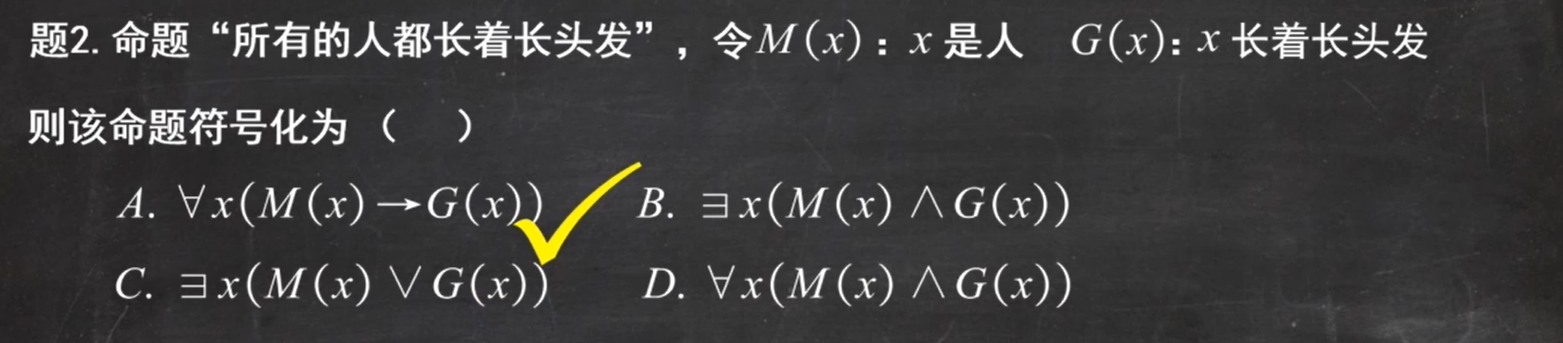
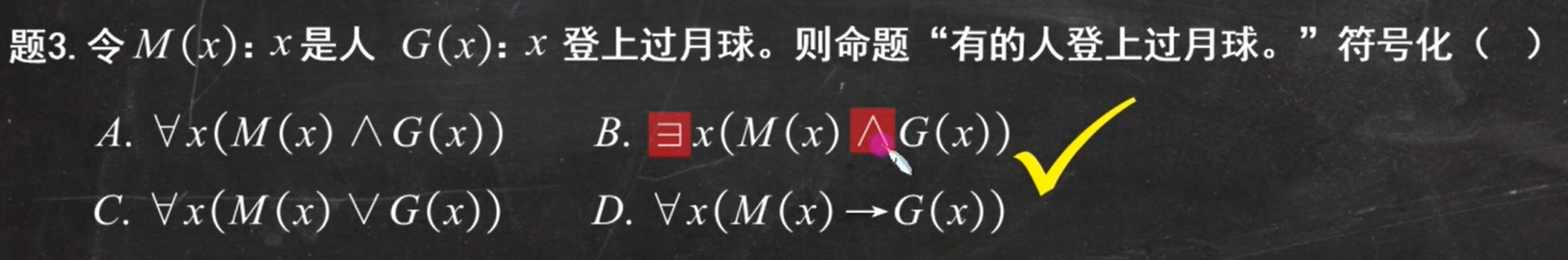
例题4、例题5:
考察符号化


2、谓词逻辑公式及其解释
指导变元、辖域、约束出现、自由出现

例题1:

解1、解2:


给出永真式、永假式、可满足式的定义

注意:当多个量词出现的时候,他们的顺序不能随便调换(存在任意和任意存在是不等价的)
例题2:

第五章(谓词逻辑等值演算与推理)
1、谓词逻辑等值式与置换规则

下面给出谓词逻辑中的基本等值式
(1)量词否定等值式

(2)量词辖域收缩与扩张等值式

(3)量词分配等值式
注意:任意和合取一起、存在和析取一起可以双向,反之只能单向
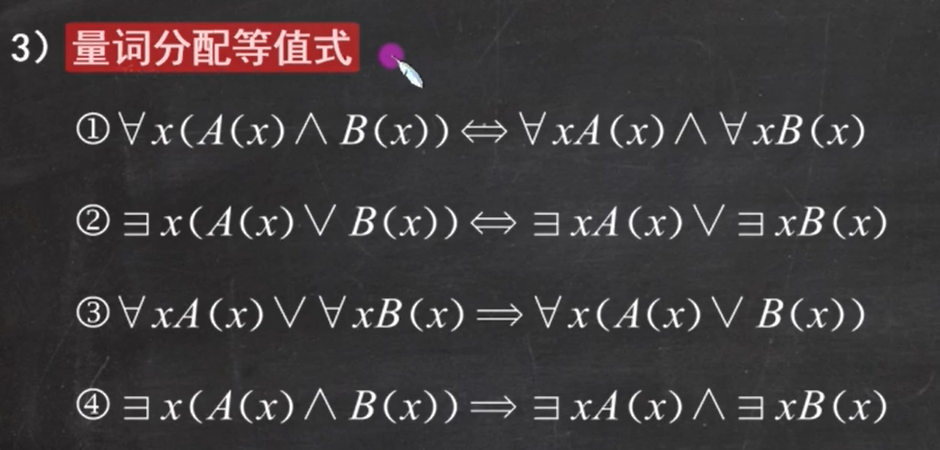
(4)命题逻辑中的重言式的代换都是谓词逻辑中的永真式

例题1:

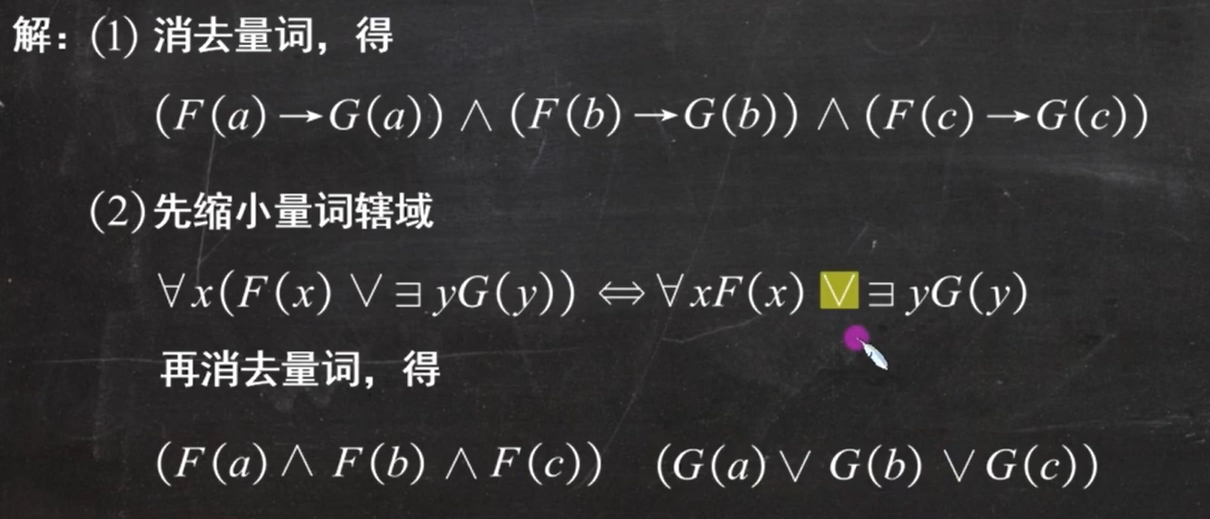
如果同时出现存在、任意,先消去后面的,从里向外
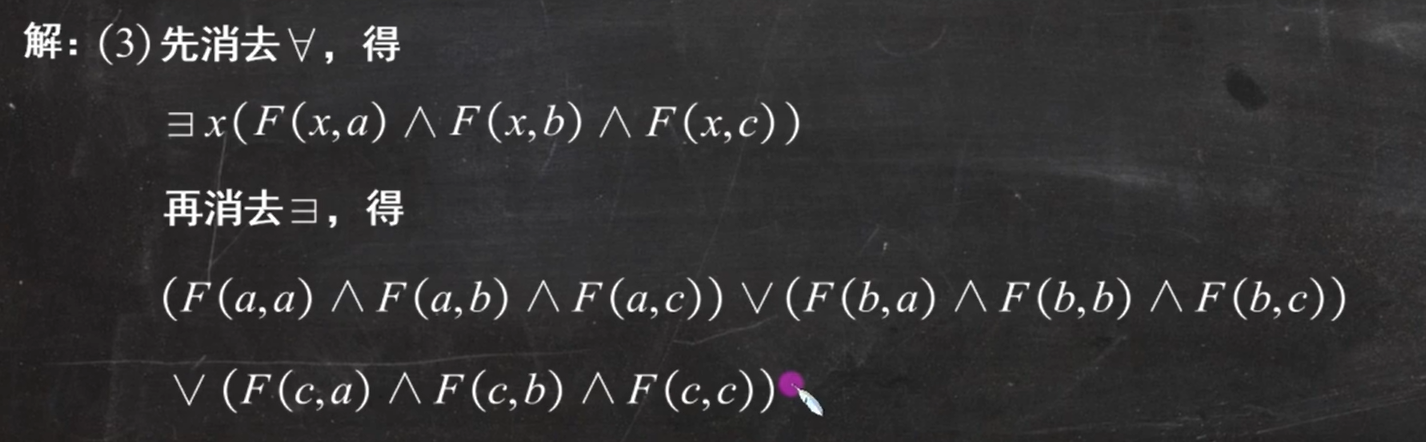
例题2:

例题3:

2、谓词逻辑前束范式
什么是前束范式?就是所有的存在量词、全称量词写在最前面
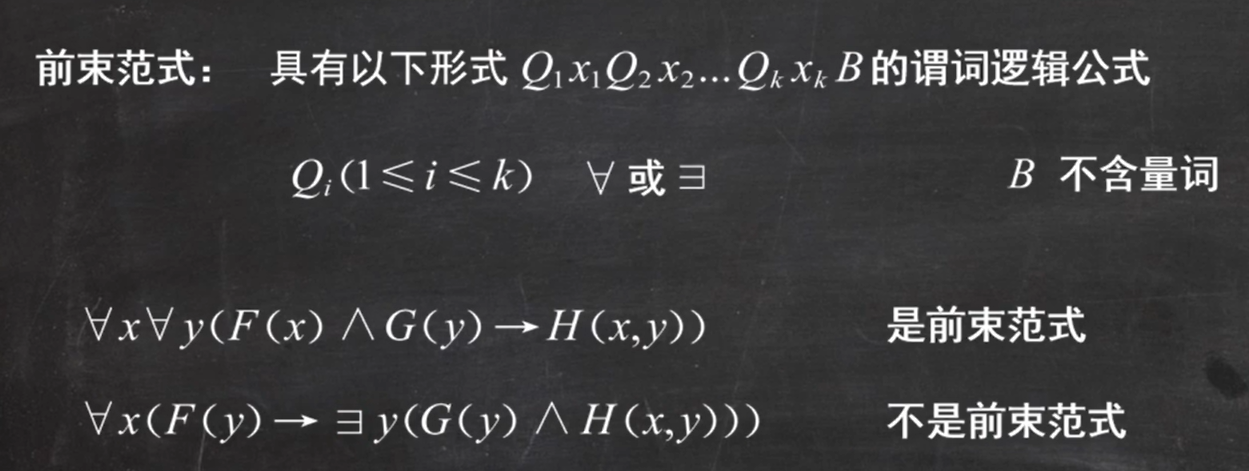
谓词逻辑中的任何公式都存在等值的前束范式!
例题1:
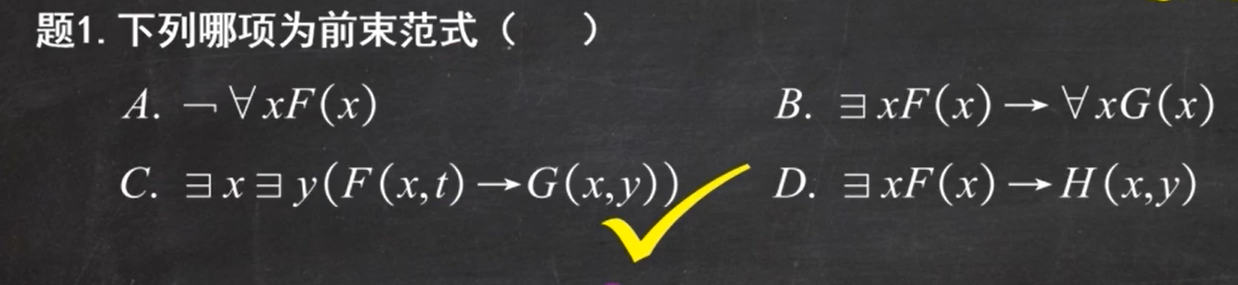
例题2:

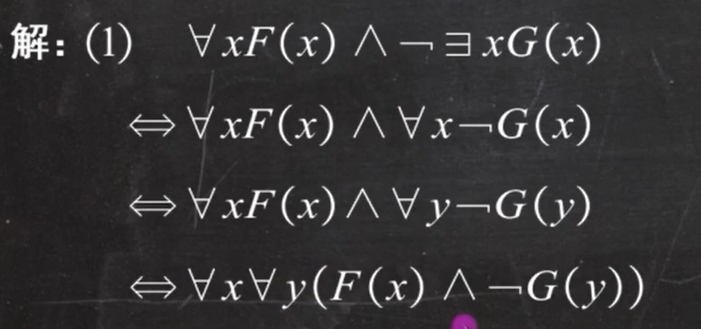
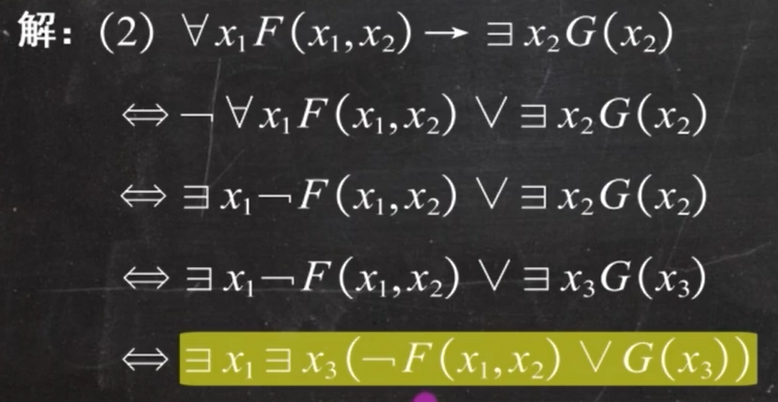
3、谓词逻辑的推理理论

相关公式:
①命题逻辑推理定律的代换实例

②由基本等值式生成的推理实例

③一些常用的重要推理定律

④4条消去量词和引入量词的规则

例题1:
推理证明(我们写的时候可以通过消去和引入的方法来忽视量词,最后推导出来再写上)

注意,存在量词的消去一定要在全程量词的消去之前(图中第②步和第⑥步)
例题2:
结论中有蕴含,那么可以附加蕴含式的左边为附加前提
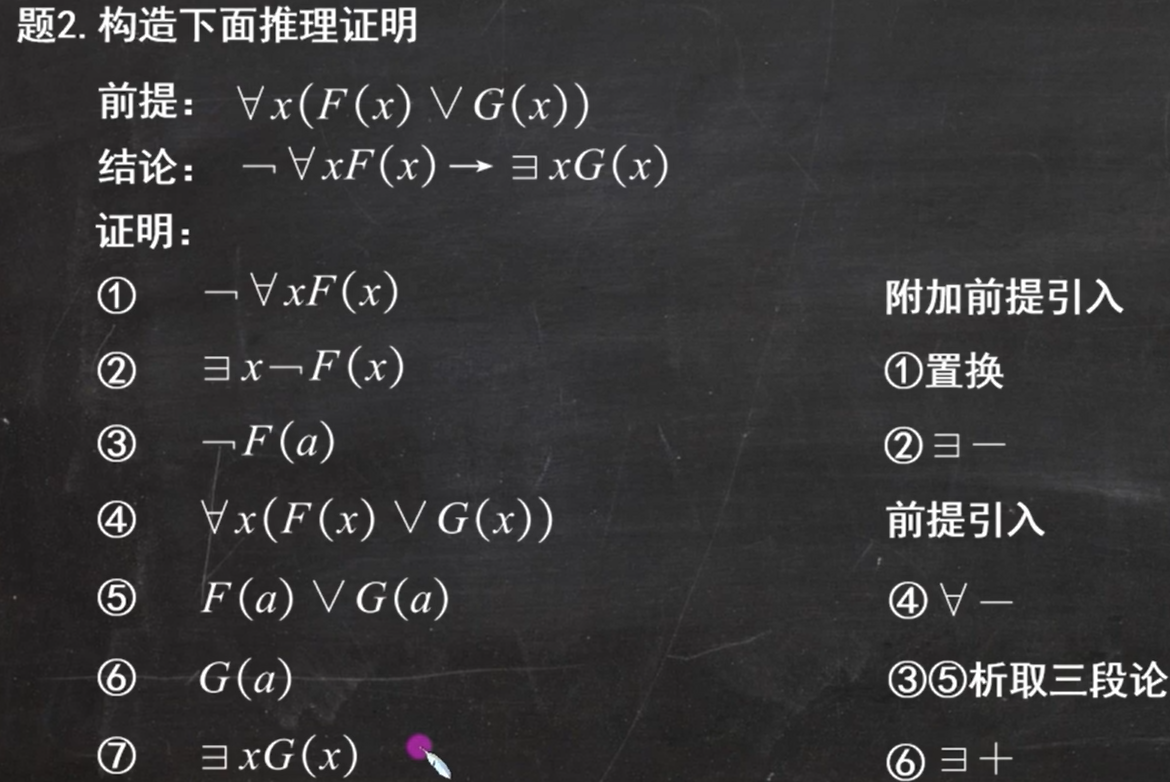
例题3:
自然语言谓词逻辑推理证明
先进行命题符号化
再使用归谬法获得一个额外的前提

第六章(集合代数)
1、集合的基本概念
∈ 符号的概念
子集、真子集、x元子集的概念
空集的概念
幂集的概念P(A),幂集有2的n次方个元素
全集的概念
例题1:

例题2:

2、集合的运算
最基本的交并补
对称差集(并的减交的)、绝对补集(全集减去自己)、广义并(自己的元素相并)、广义交(自己的元素相交)
例题1:

例题2:
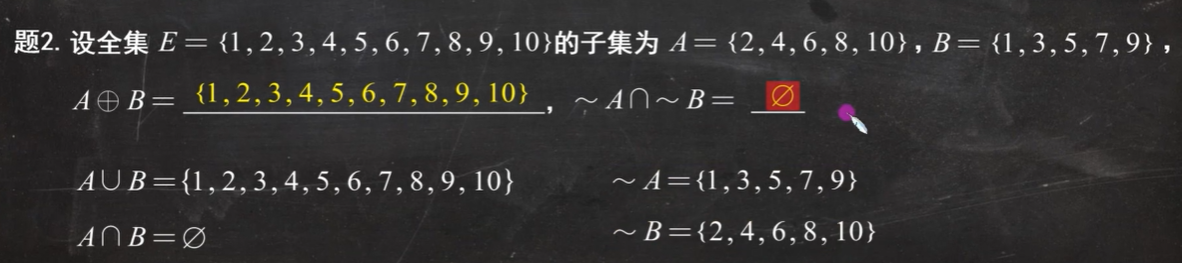
3、有穷集的计数
自然语言转化为符号语言
然后画图!
例题:

先画图:
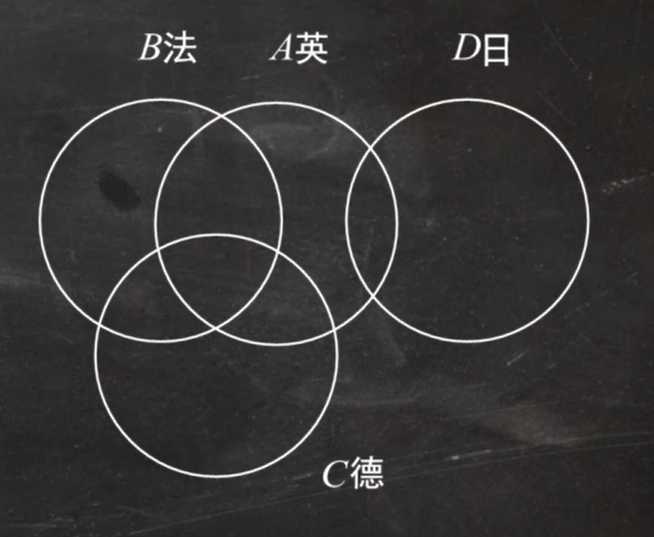
然后根据设出来的值进行补充图像:

接着列方程:
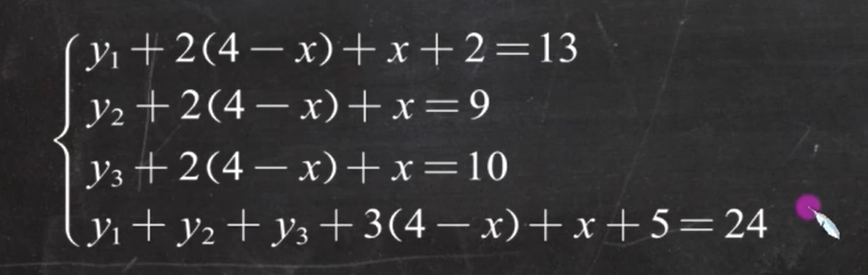
解方程:
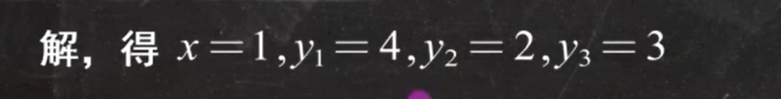
包含排斥原理:
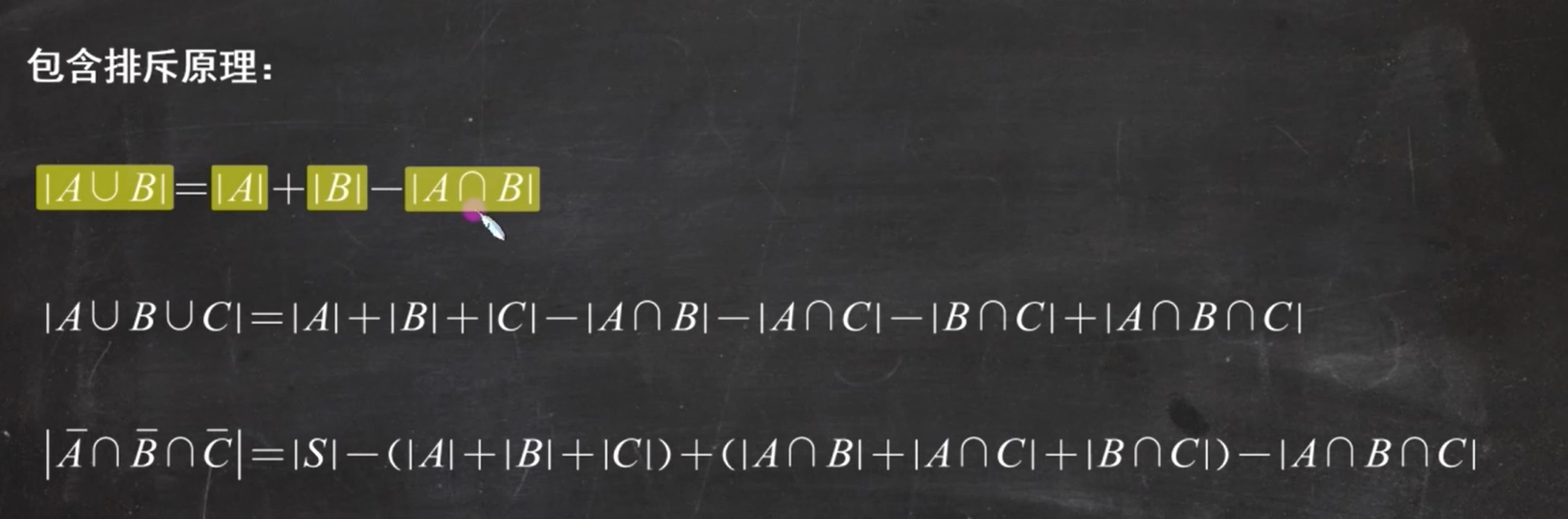
发现和概率论中的:**P(A∪B)=P(A)+P(B)-P(AB)**是一样的!连在一起记忆~
例题2:

4、集合恒等式
就是概率论中的知识点咯

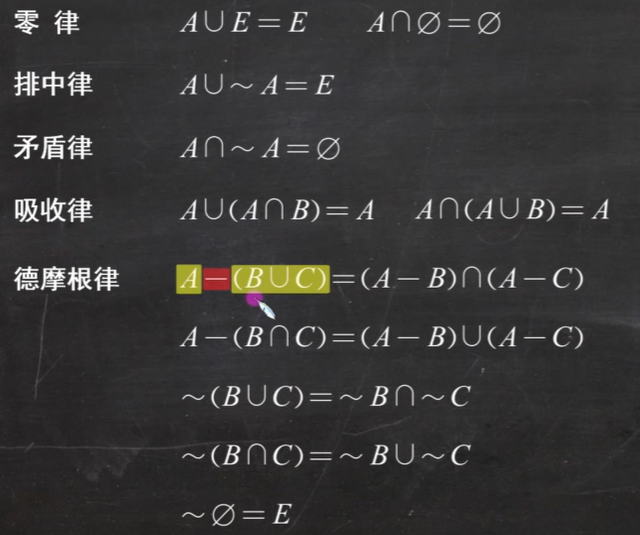
需要记住一个 A - B = A ∩ ~B,其实也很好理解
重要公式:
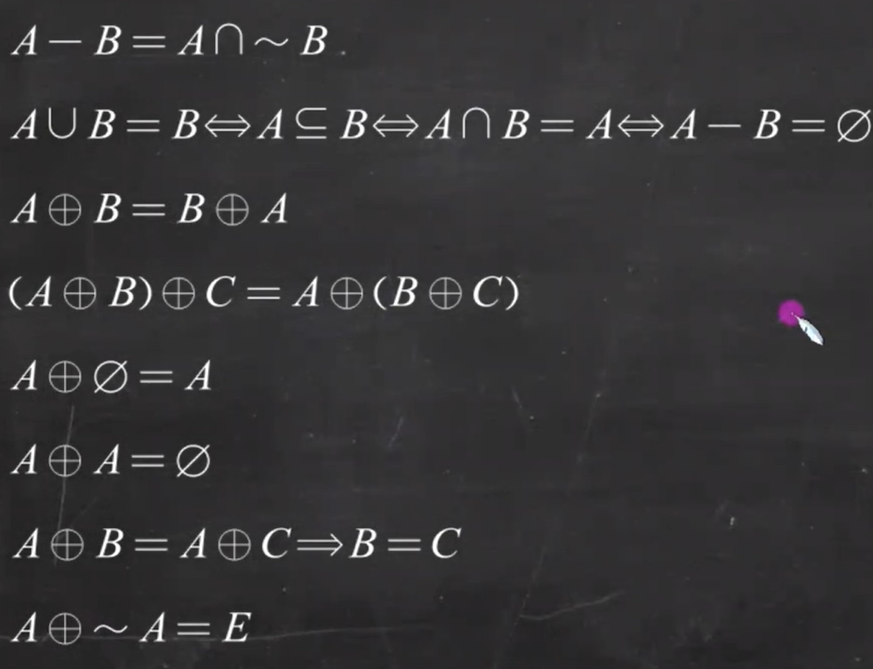
例题1:
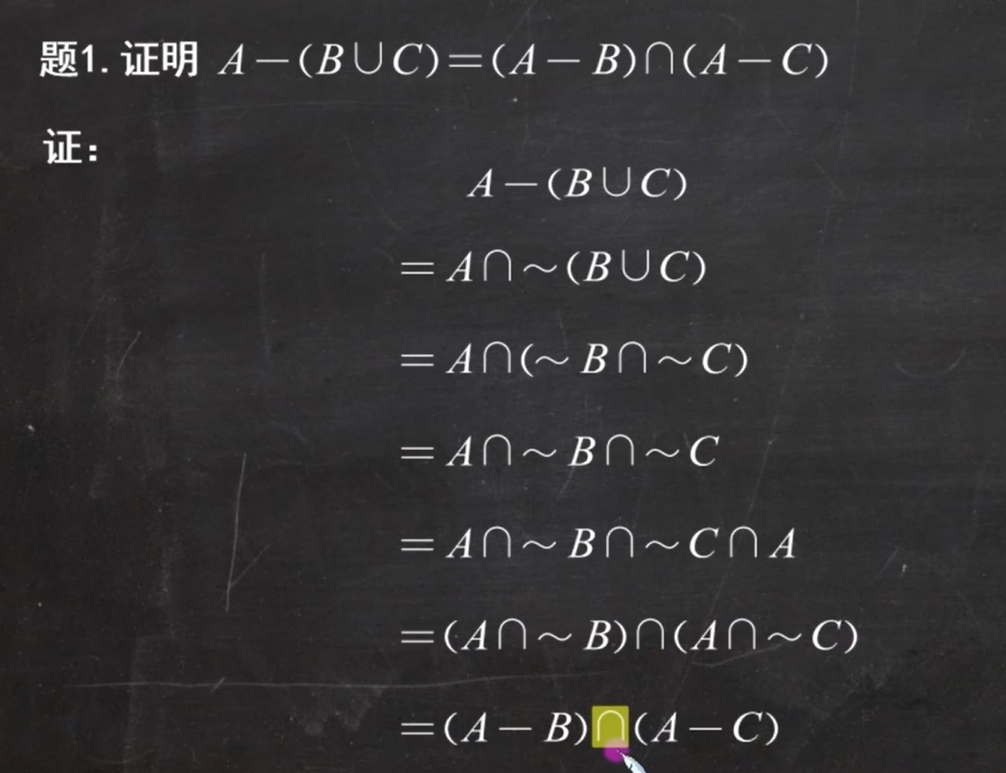
第七章(二元关系1)
1、有序对、笛卡尔积
有序对的第一元素x、第二元素y

例题1:
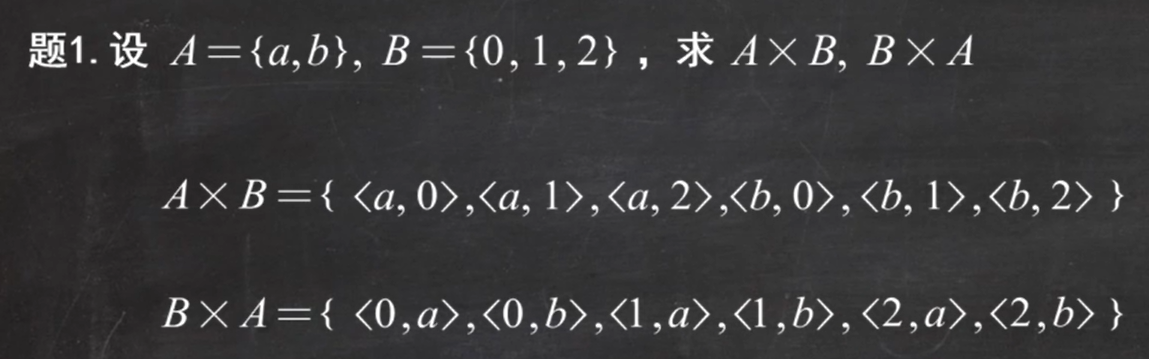
笛卡尔积不满足交换律
笛卡尔积的元素个数:

笛卡尔积只满足对并、交的分配律运算

2、二元关系
如果一个集合满足下面条件之一就是二元关系:
- 集合非空,并且它的元素都是有序对
- 集合是空集
A,B是集合,那么A×B的任何子集所定义的二元关系称作从A到B的二元关系
A上有2的n的平方次方个不同的二元关系

例题1:

例题2:

A上的特殊关系:空关系、全域关系EA、恒等关系IA
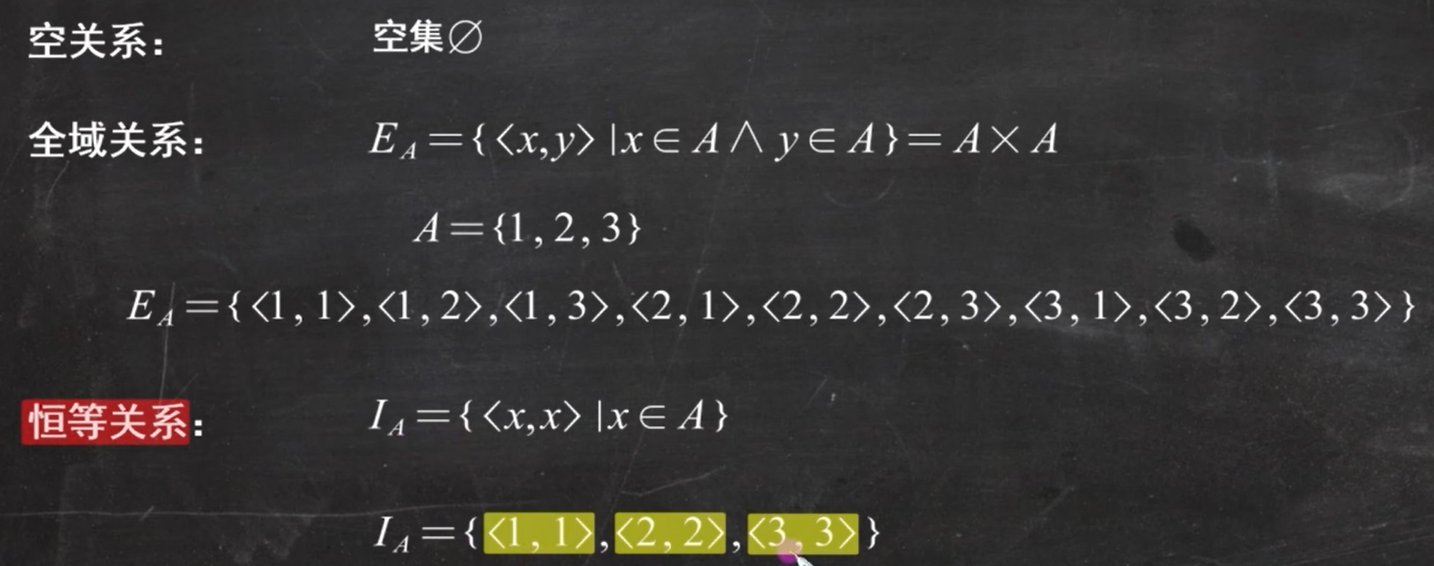
表示集合的方法(三种):集合表达式、关系矩阵、关系图
例题1:
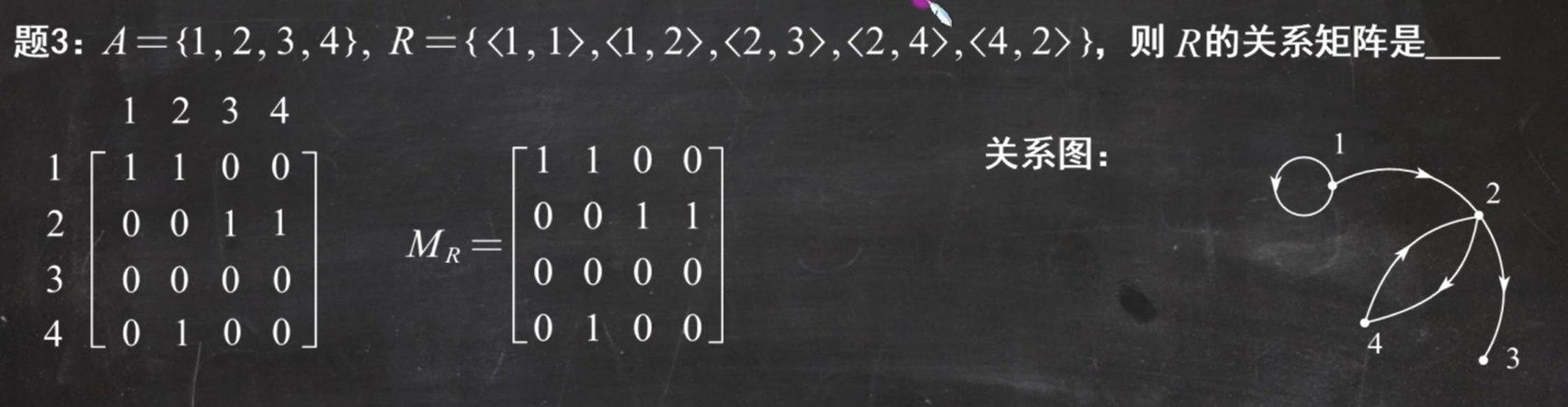
例题2:

3、关系的运算
设R为二元关系,那么有
- 定义域:R中所有有序对的第一元素构成的集合,记作domR
- 值域:R中所有有序对的第二元素构成的集合,记作ranR
- 域:R中定义域和值域的并集,记作fldR
- R的逆关系:简称R的逆,记作R的-1次方
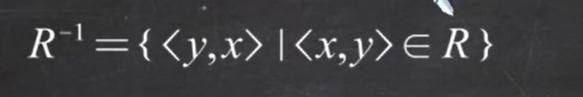
- 设F、G为二元关系,G对F的右复合记作FoG
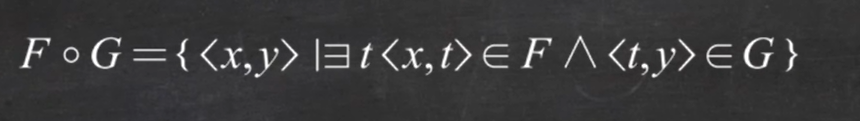
例题1: (域关系)
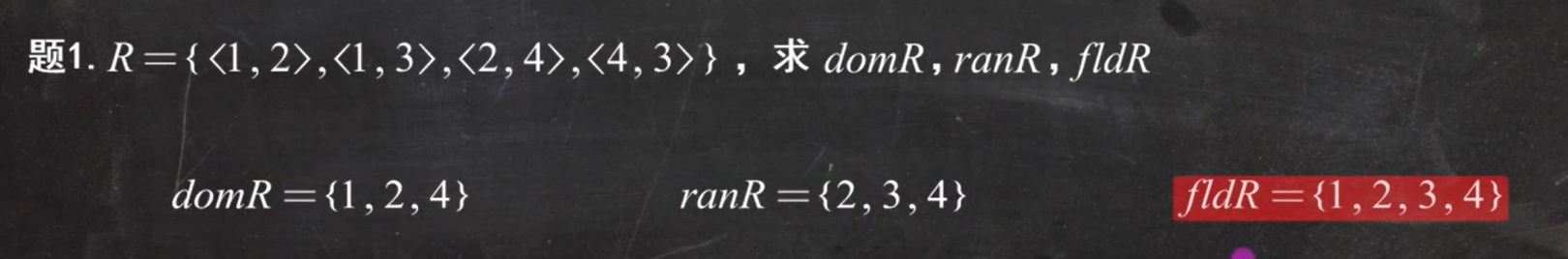
例题2:(右复合)
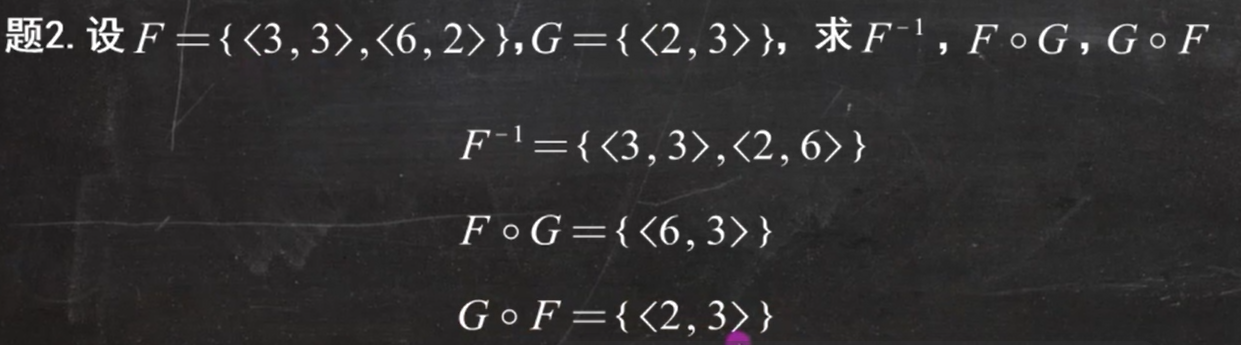
第八章(二元关系2)
1、关系的性质
自反、反自反(所有的有序对都不满足自反)
对称、反对称(所有的有序对都不满足对称)
传递(例如:**R={<1,2><2,3><1,3>}**在一个集合中,那么这个集合具有传递性)
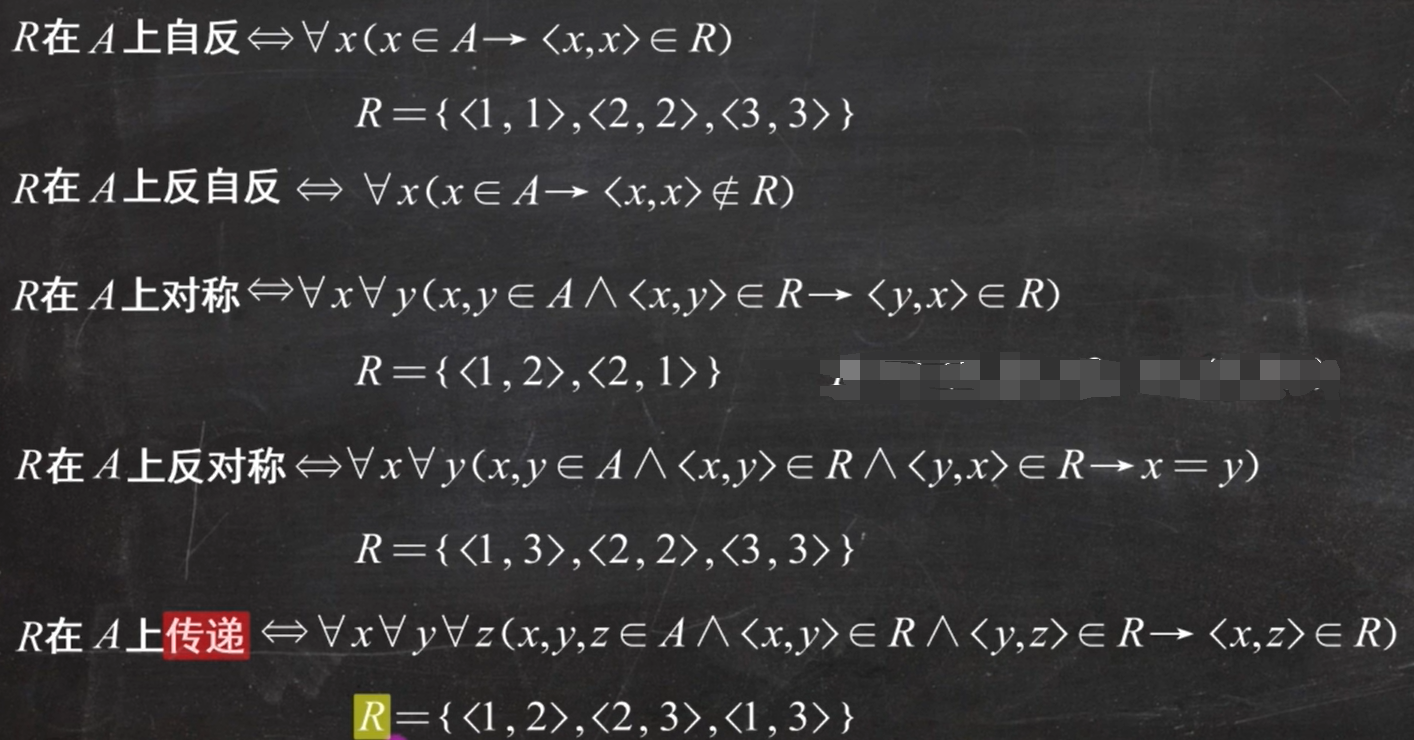


例题1:
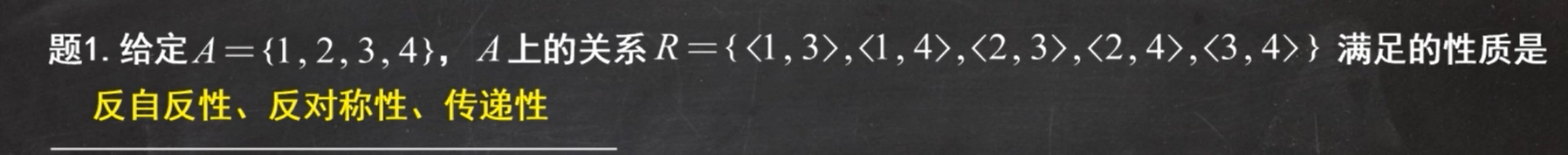
反对称是因为,R和R-1向交得到的是空集,空集是IA的子集,有反对称性
例题2:

例题3:(关系图)

例题4:(关系矩阵)

2、关系的闭包
自反(对称、传递)闭包概念

例题1:
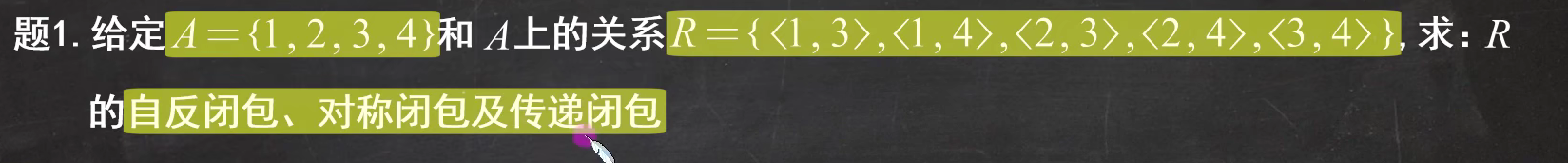

原集合本来就是具有传递性的,所以传递闭包就是它自己
3、等价关系与划分
等价的概念:设R是非空集合A上的关系,如果R是自反的、对称的和传递的,那么称R为A上的等价关系

例题1:(等价类的例子)

引入商集的概念

划分的概念(pai是P(A)幂集的子集)
简单来说就是,广义并(但不能有交集)是原集合就是一个划分
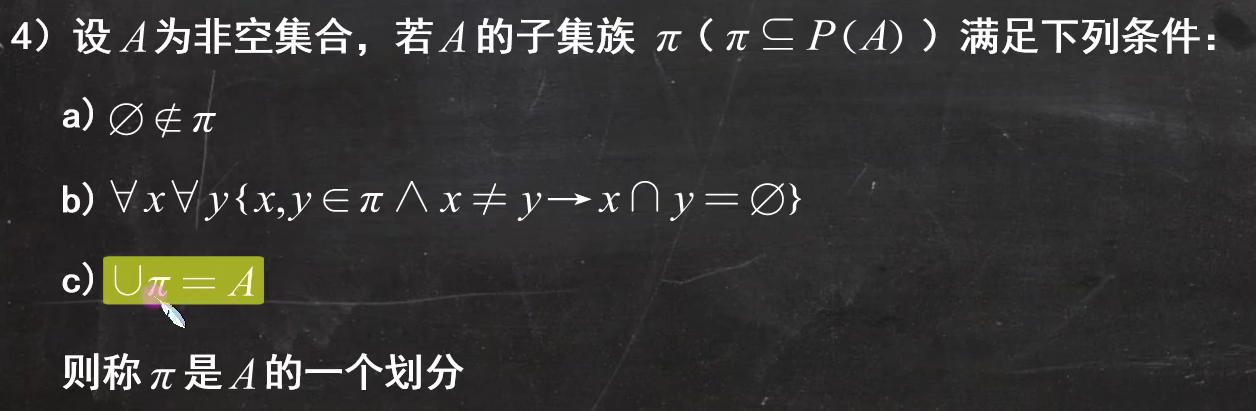
例题2:(判断划分)

例题3:

有多少种划分,就有多少种等价关系
例题4:

4、偏序关系
如果集合A中的关系R是自反的、反对称的、传递的,那么R是A上的偏序关系

例题1:(哈斯图)
如何画哈斯图?


在这里引入——最大元和最小元的判定:

上一个例题中的解释:

之所以没有最小元是因为在哈斯图同一个阶层的点是不可比的,就没有同阶的最大元和最小元之说~
接下来引入——极大元和极小元的概念解释。

仍然是拿上一个例题出来解释:
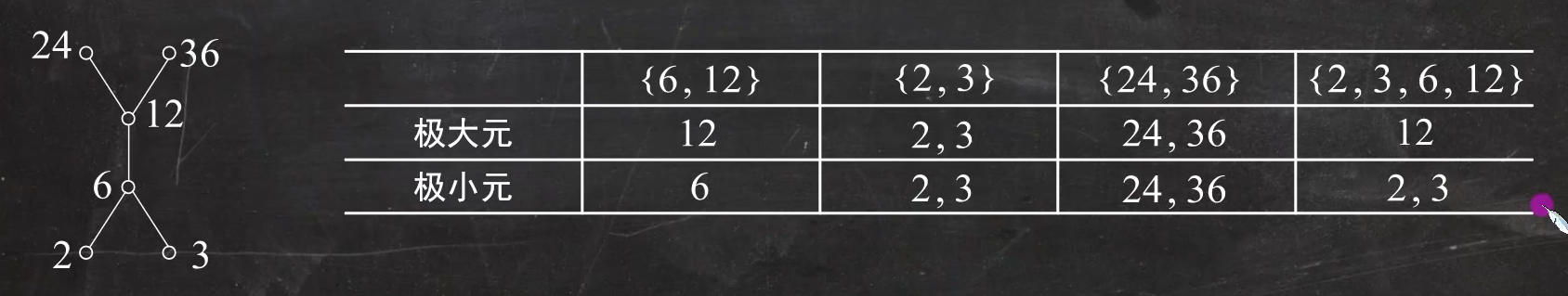
需要注意的是,在极小元和极大元的判定中即使在同一阶层也可以相比,没有不可比的概念。
哈斯图中的孤立顶点不仅是极小元也是极大元
接下来引入——上界和上确界的概念:

还是那个例子

接下来引入——下界和下确界的概念:(和上界的概念是类似的)


上界、上确界、下界、下确界是不一定存在的!
第九章(函数)
1、函数的定义与性质
- x是F定义域中的元素,y是F值域中的元素

例题1:(判断函数)
简单的对应关系

- f:A->B 是 从A到B的函数
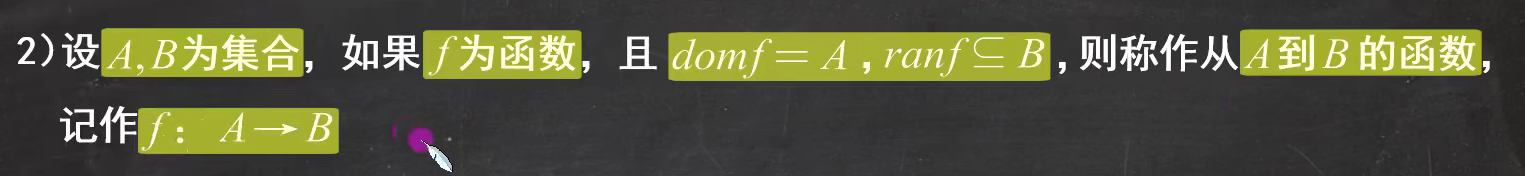
- 满射、单射、双射(看图理解)
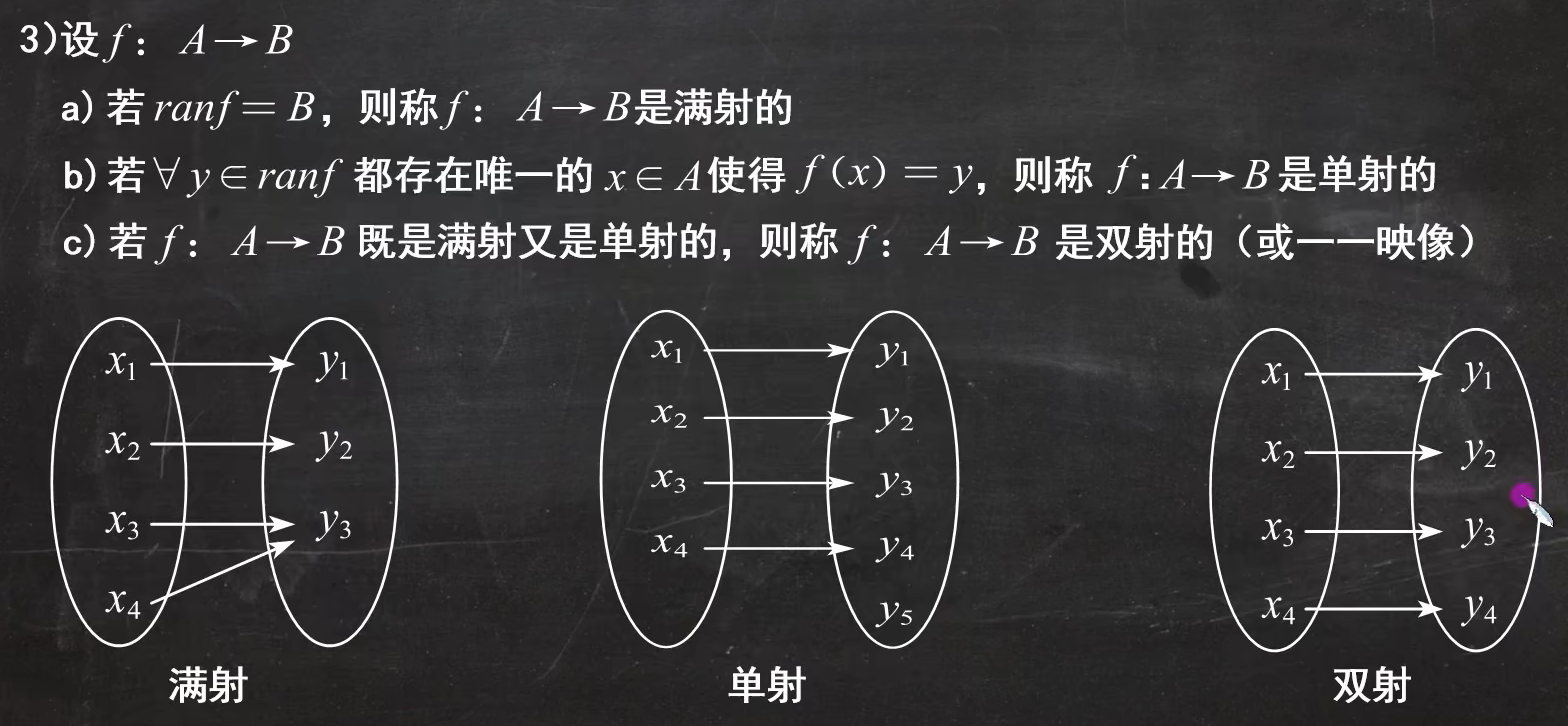
- 满射、单射、双射的必要条件(还是很好理解)
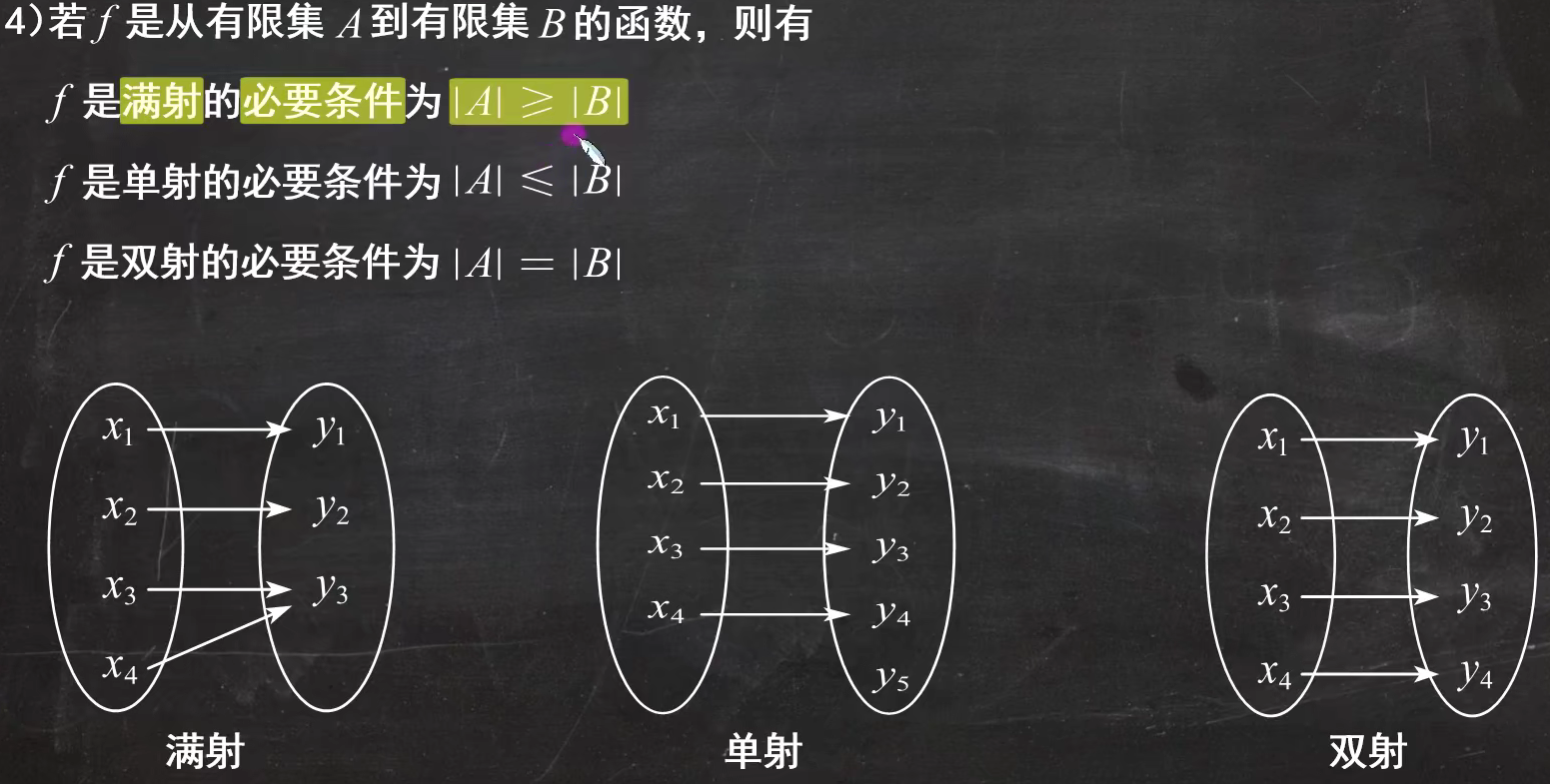
例题2:
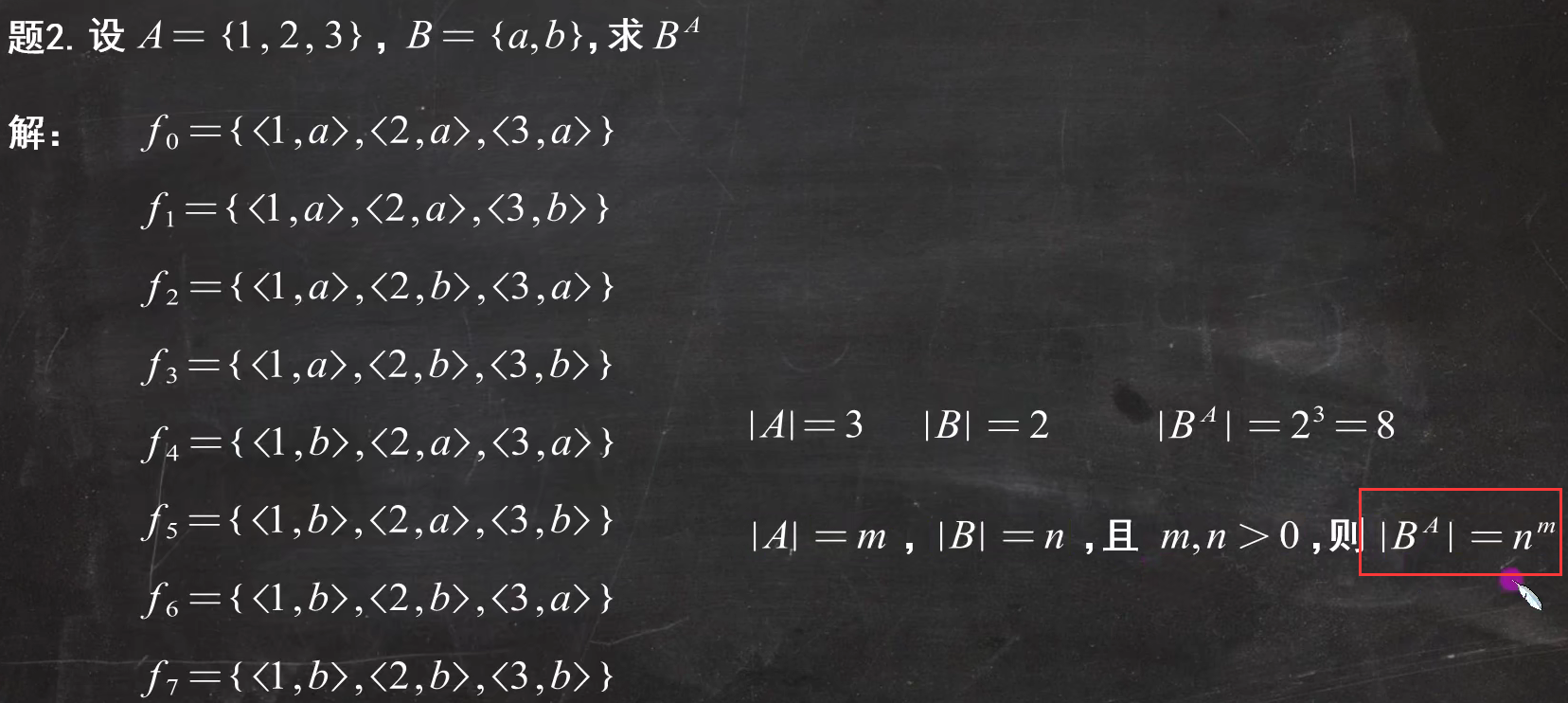
例题3:

2、函数的复合与反函数
定义如下:
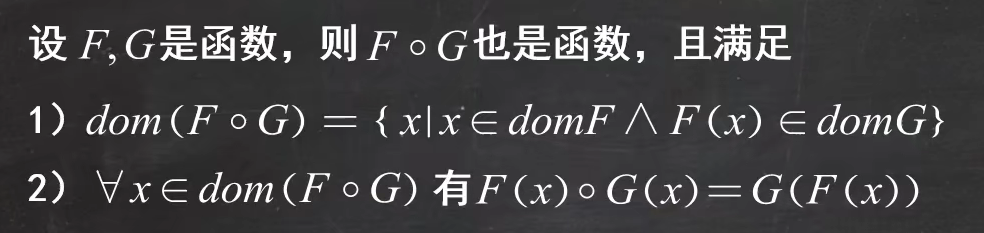
例题1:

复合运算具有结合律

为什么fx在gx里面,其实也很好理解,首先是进行f到g的右复合,那么肯定是首先算括号里的fx,再算gx,所以是如上的形式。
例题2:
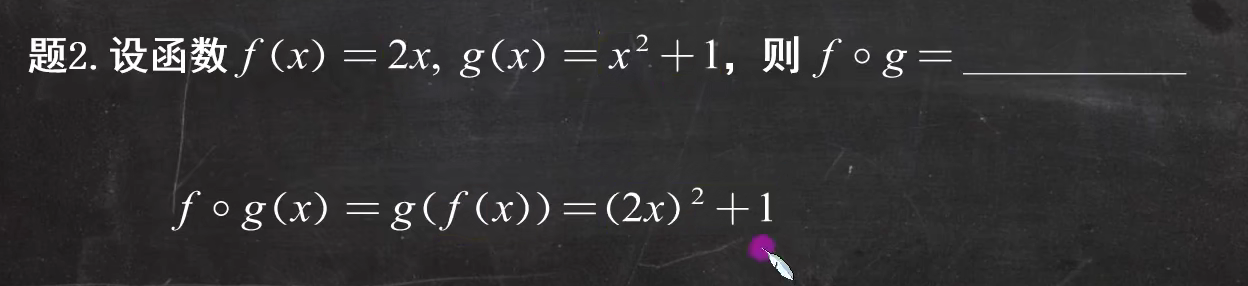
接下来引入反函数的概念:(就是数学中的那套)
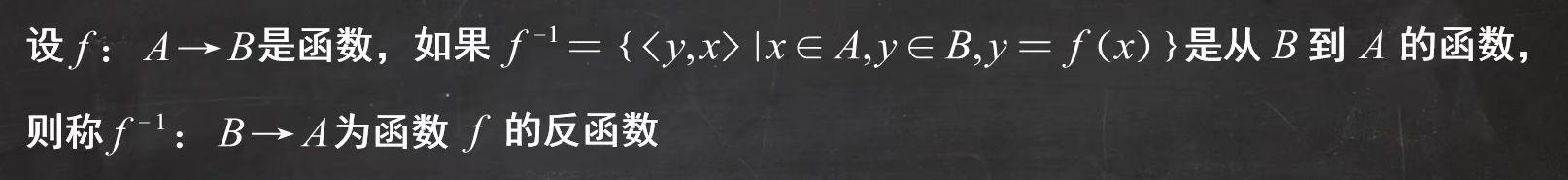

之所以没有反函数,是因为反过来存在x对应多个y,不满足函数的定义
第十章(图)
1、图
无向图、有向图、图的阶(n个顶点的图称作n阶图)、零图、平凡图
图 G=<V,E>,V是点集,E是边集
端点、关联、相邻
图的度数(顶点作为边的端点的次数)
入度(顶点作为边的始点)d+(v)、出度(顶点作为边的终点)d-(v)
度数 = 入度 + 出度
握手定理:
-
任何无向图中,所有顶点的度数之和等于边数的两倍
-
任何有向图中,所有顶点的度数之和等于边数的两倍
所有顶点的入度之和等于所有顶点的出度之和,都等于边数
-
推论:任何图中,奇度顶点的个数是偶数个
例题1:

例题2:(度序列)

例题3:(可图化充要条件是度数之和为偶数)

例题4:(简单可图化的充要条件加上了,最大度≤顶点数-1)

无向完全图就是每个顶点对应其余的n-1个顶点相邻
n阶无向完全图边的条数为n(n-1)/2
例题5:

2、通路与回路
通路:无向图中顶点和边的交替序列
回路:交替序列的第一个顶点和最后一个顶点相同
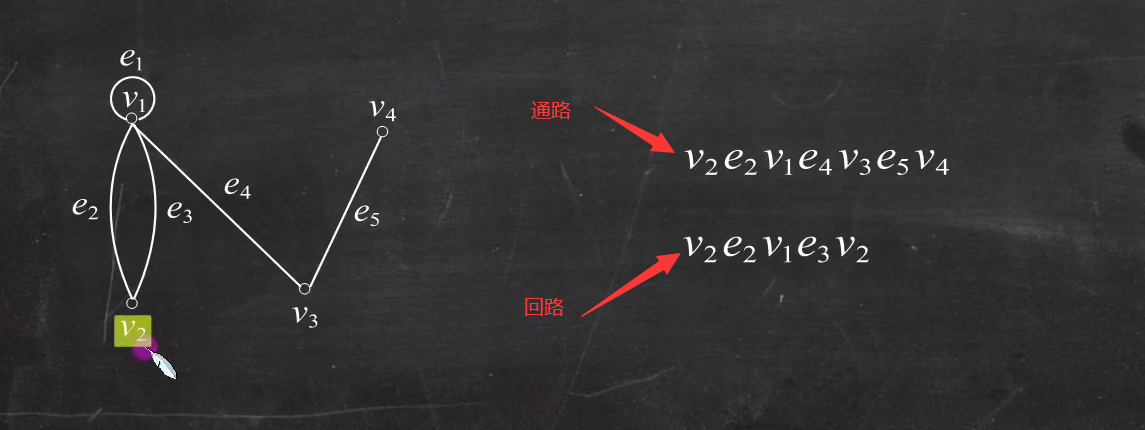
3、图的连通性
-
连通的概念:如果无向图中2个顶点之间存在通路,那么这两个点就是连通的
连通图的概念:无向图中任意两个顶点都是连通的(或者无向图G是平凡图)
-
可达的概念:有向图中2个顶点u、v存在通路,那么u到v是可达的
如果u、v存在通路,v、u也存在通路,那么是互相可达
-
强连通、单项连通、弱连通

例题1:

4、图的矩阵表示
无向图的关联矩阵的定义:
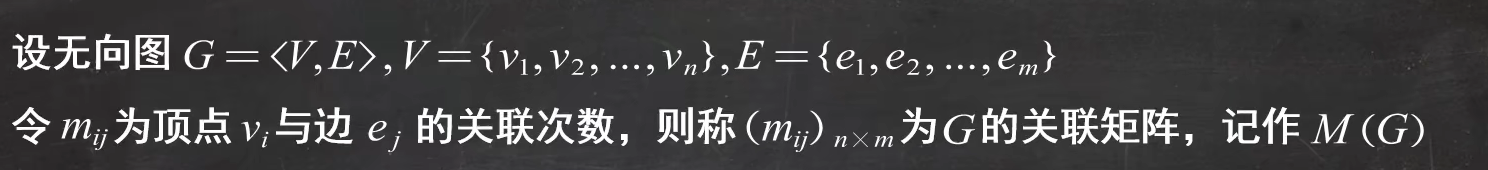
例题1:(无向图的关联矩阵)
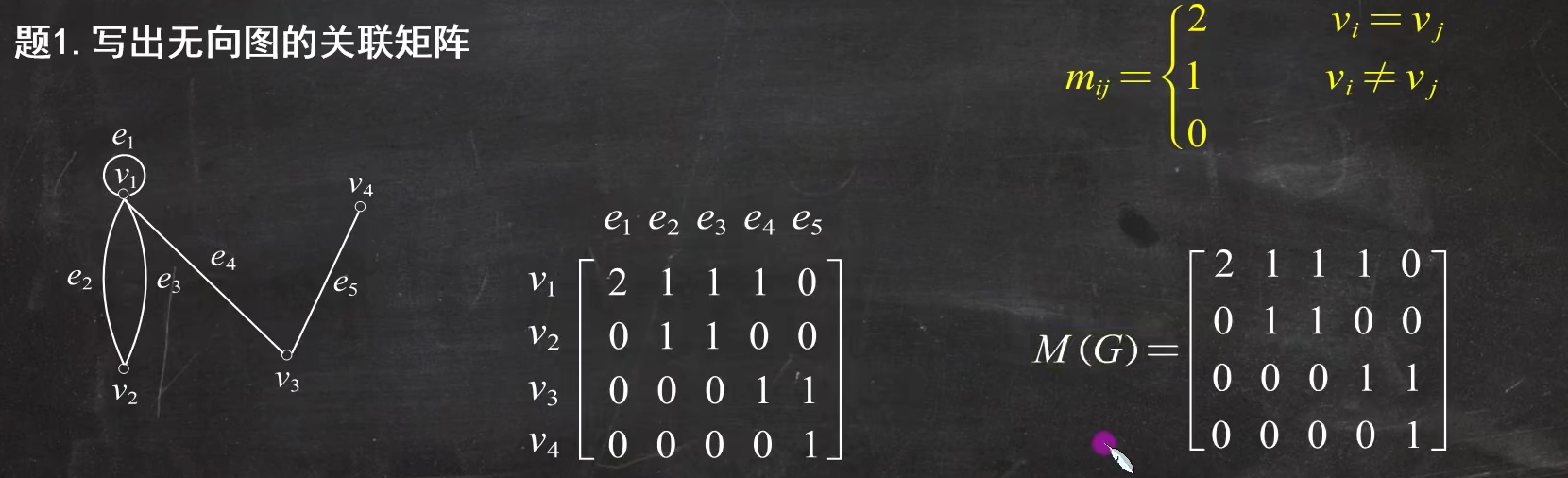
有向图的关联矩阵的定义:
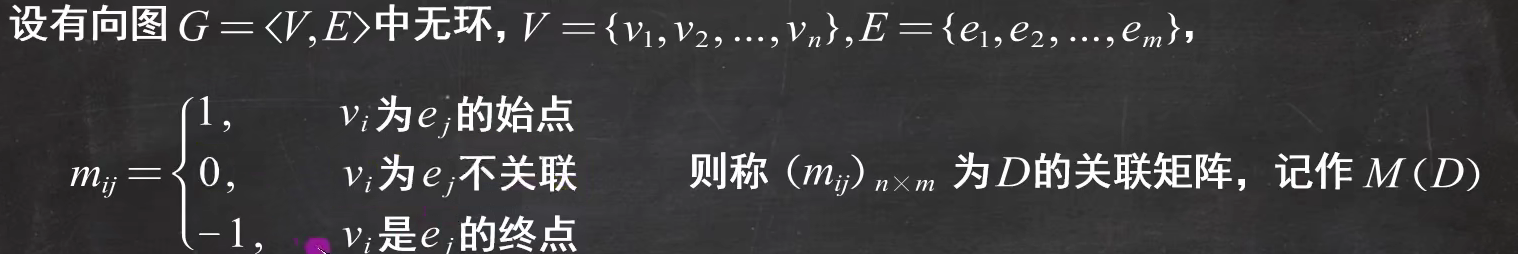
例题2:(有向图的关联矩阵)
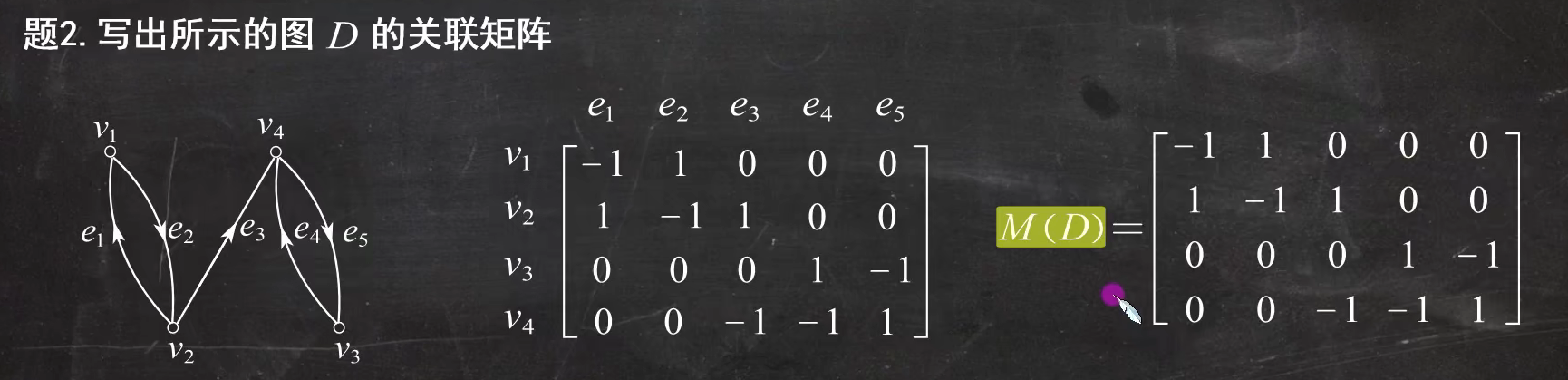
有向图的邻接矩阵的定义:(顶点到顶点的关系)

例题3:
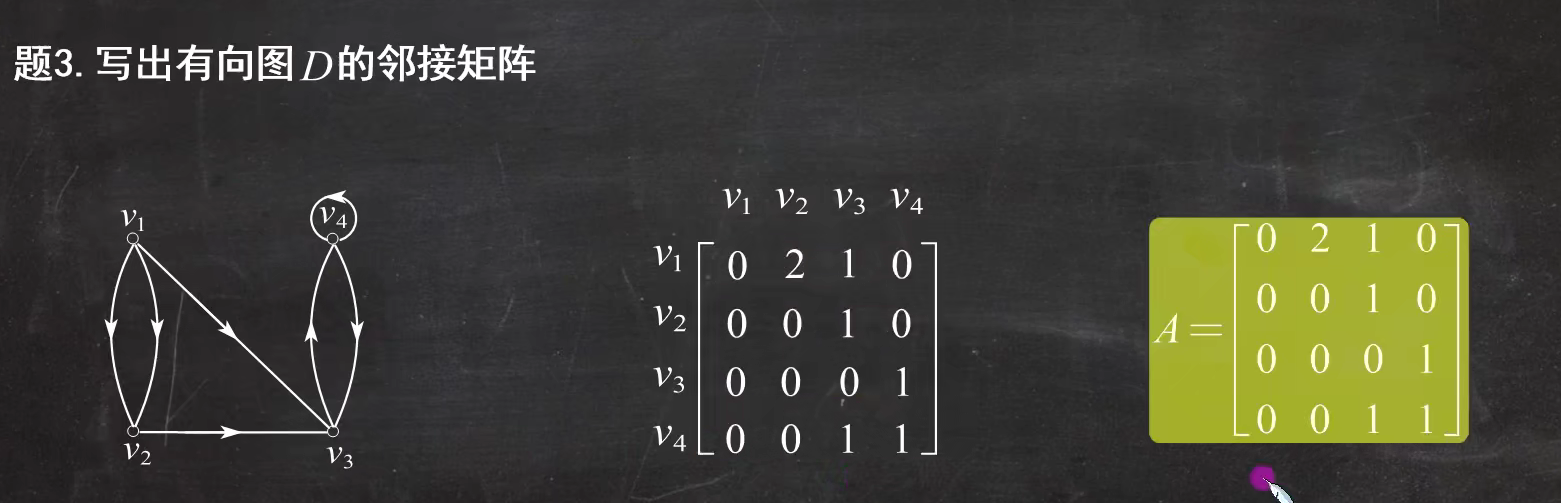
如何判断通路条数和回路条数?


可达矩阵:(一个点是否可以到另一个点)
可达矩阵的主对角线的元素全是1

第十一章(欧拉图与哈密顿图)
1、欧拉图
各种概念解释:
欧拉通路:通过图中所有边且仅一次的通路
回路同上一样的定义
欧拉图就是具有欧拉回路的图(强调边的关系)
半欧拉图就是仅仅具有欧拉通路但是没有欧拉回路的图
无向图是欧拉图的充要条件——G是连通图且没有奇度顶点
有向图是欧拉图的充要条件是——D是强连通图并且每个顶点入度等于出度
例题1:(欧拉图是和边的关系)

例题2:

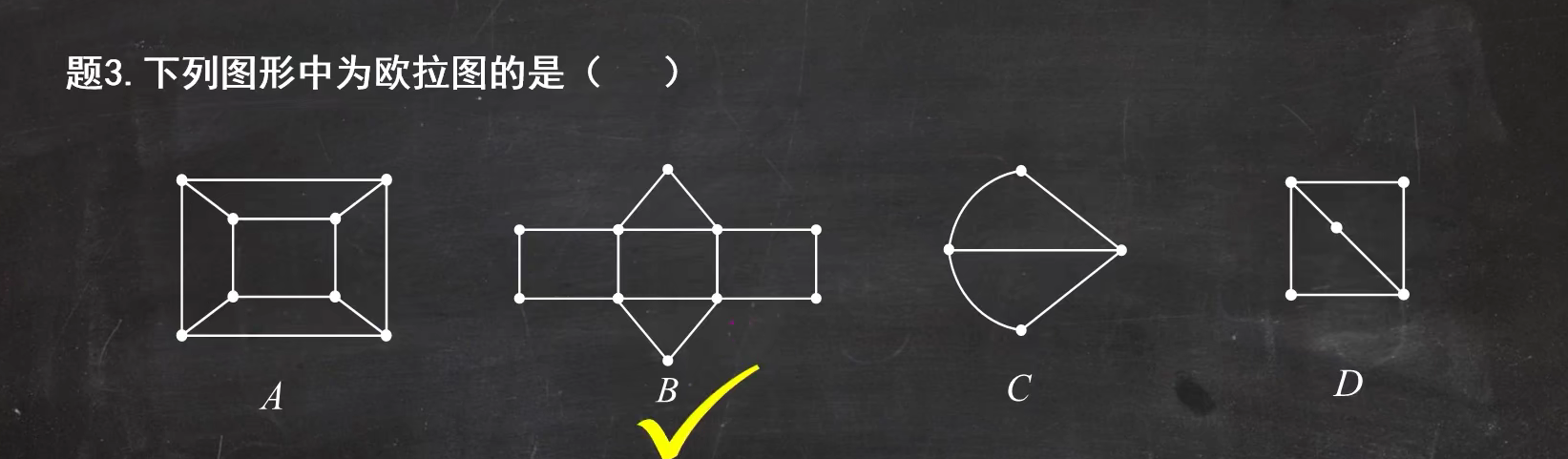
例题3:(判断欧拉图)
一个图中如果出现奇度顶点,那么一定不是欧拉图
附带一个可能会用到的欧拉公式:

2、哈密顿图
- 哈密顿通路:经过图中所有的顶点一次且仅一次的通路
- 哈密顿回路:经过图中所有的顶点一次且仅一次的通路
- 哈密顿图:具有哈密顿回路的图(强调点的关系)
- 半哈密顿图:具有哈密顿通路但是没有哈密顿回路的图
- 没有简单的充要条件
- 充分条件,有(度数)d(u)+d(v)>= n-1,则存在哈密顿通路
- 有d(u)+d(v)>= n,则存在哈密顿回路
例题1:

例题2:
