【概率论与数理统计】期末不挂科复习笔记
概率论就是让你没有那么大的概率挂科...
【概率论与数理统计】期末不挂科复习笔记
只能说最好先看看老师的ppt,在看看猴博士就全懂了~
第一章(条件概率、全概率、贝叶斯公式)
1、无放回类题目
无放回,直接用C解

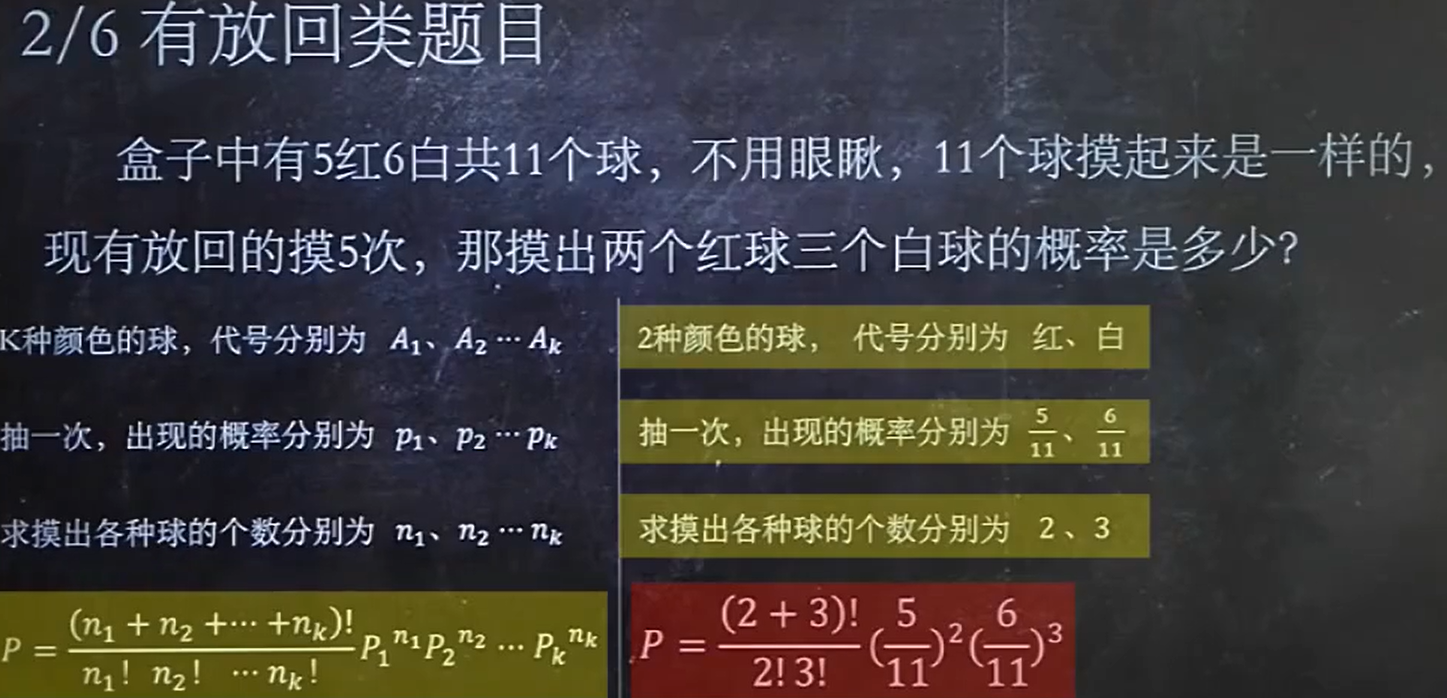
2、有放回类题目
有放回,使用(n1+n2)!/n1!*n2!然后乘上每种的概率
3、需要画图的题目

4、条件概率
A发生的前提下,B发生的概率


5、全概率公式
所有概率的总和

6、贝叶斯公式
贝叶斯其实是条件概率反过来求。其实就是已知结果求原因

可能和全概率公式结合考点,通过上一篇的P(有客车发生故障)= 0.0084来计算贝叶斯这一问。

第二章(分布函数与概率密度)
1、已知Fx(X)与fx(X)中的一项,求另一项
Fx是分布函数,fx是概率密度
小fx是大Fx求导出来的,同理可以通过小fx求积分来算大Fx
Fx求导得到fx

fx求积分得到Fx
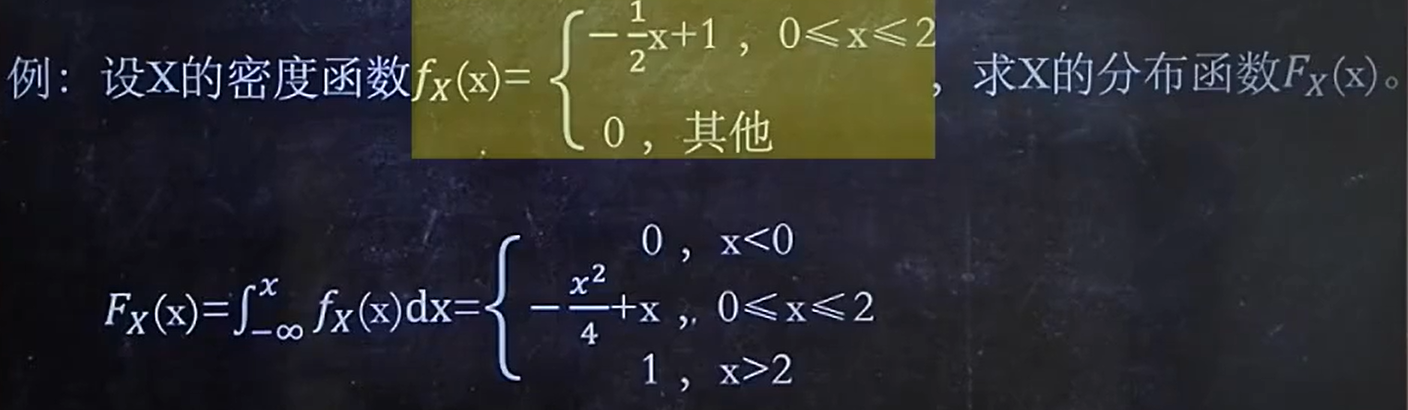
2、已知Fx(X)与fx(X)中的一种,求P
已知分布函数Fx,求概率

已知概率密度fx,求概率
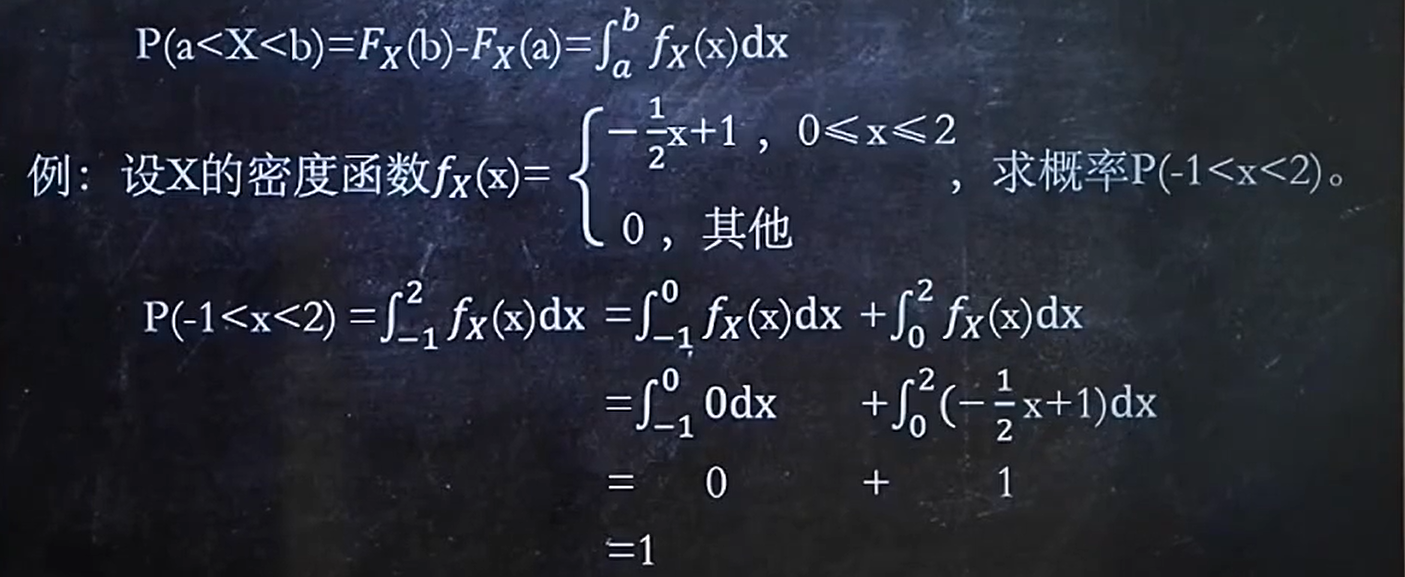
注意:P(a<X<b)和P(a<=X<=b)是等价的,这个等号不影响
3、Fx(X)或fx(X)含未知数,求未知数
记住Fx(-∞) = 0 Fx(+∞) = 1,概率密度fx(X)在-∞和+∞上的积分为1

Fx分布函数例题:
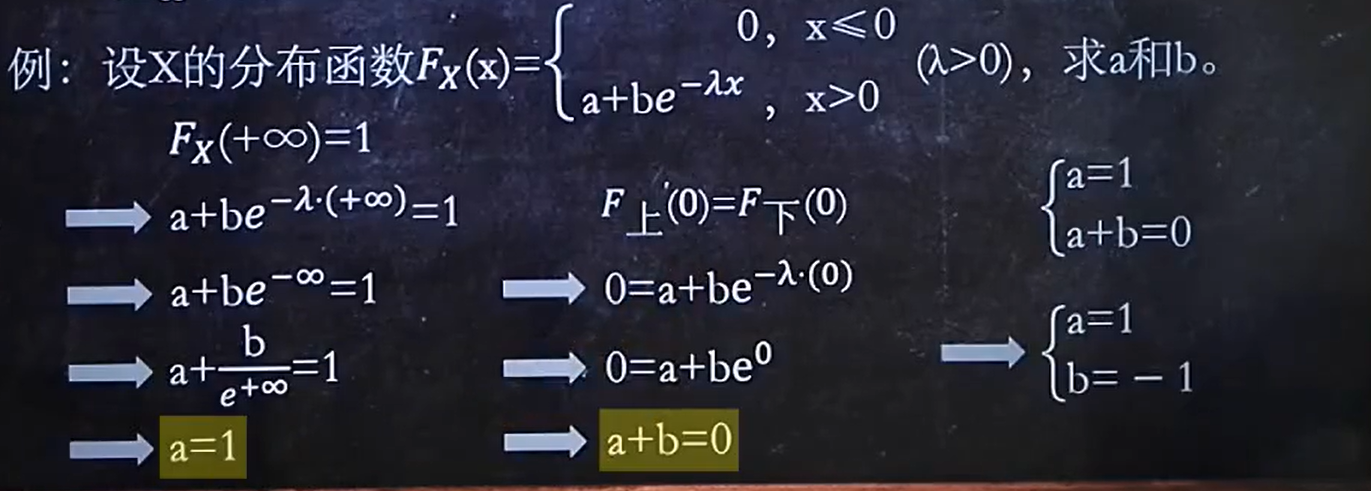
fx概率密度例题:
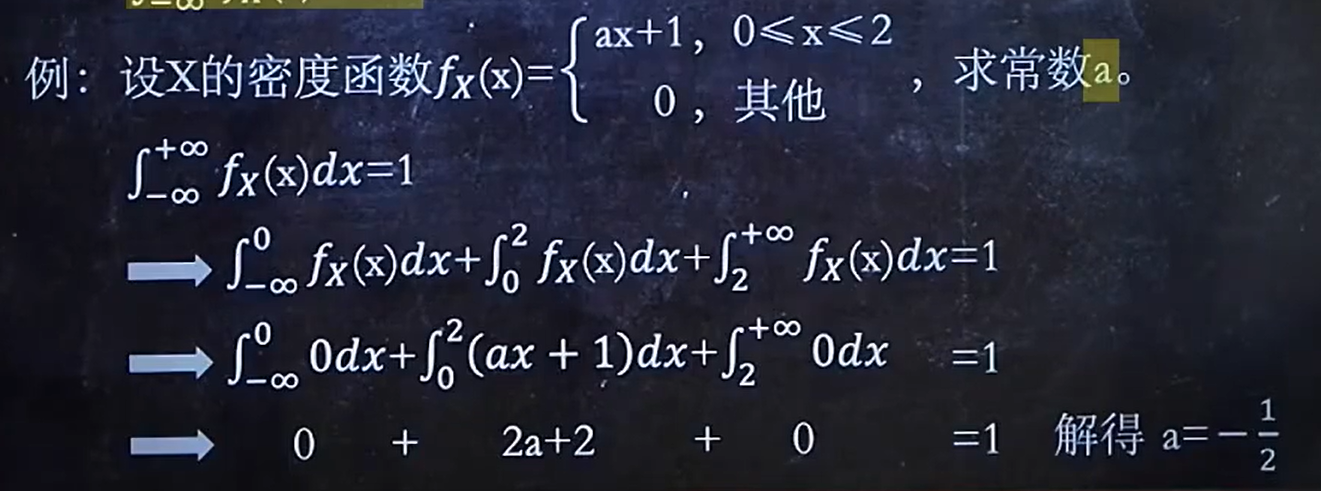
4、求分布律
高中题目了属于是,只能说dddd


第三章(分布函数与概率密度2)
1、已知X分布列,求Y分布列
替换算就完事了

2、已知Fx(X)了,求Fy(Y)
也是带入替换
- 把X换成什么什么Y
- 替换Fx(X)中的x结果为Fx(?Y)
- 判断y中是否有负号
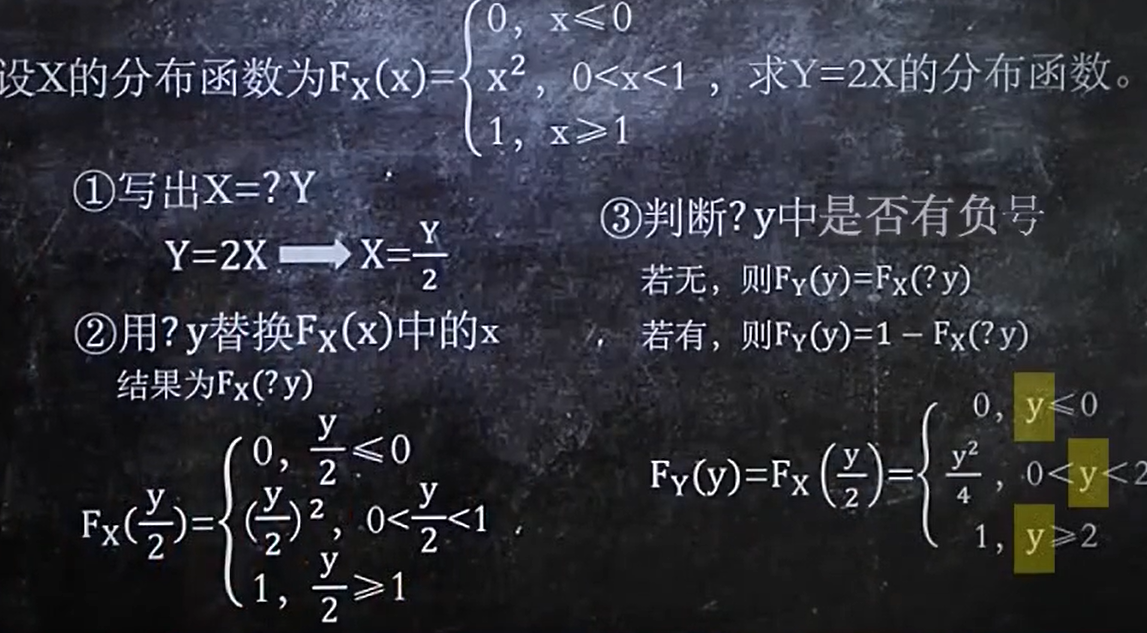
如果是带有负号,那么就这样:
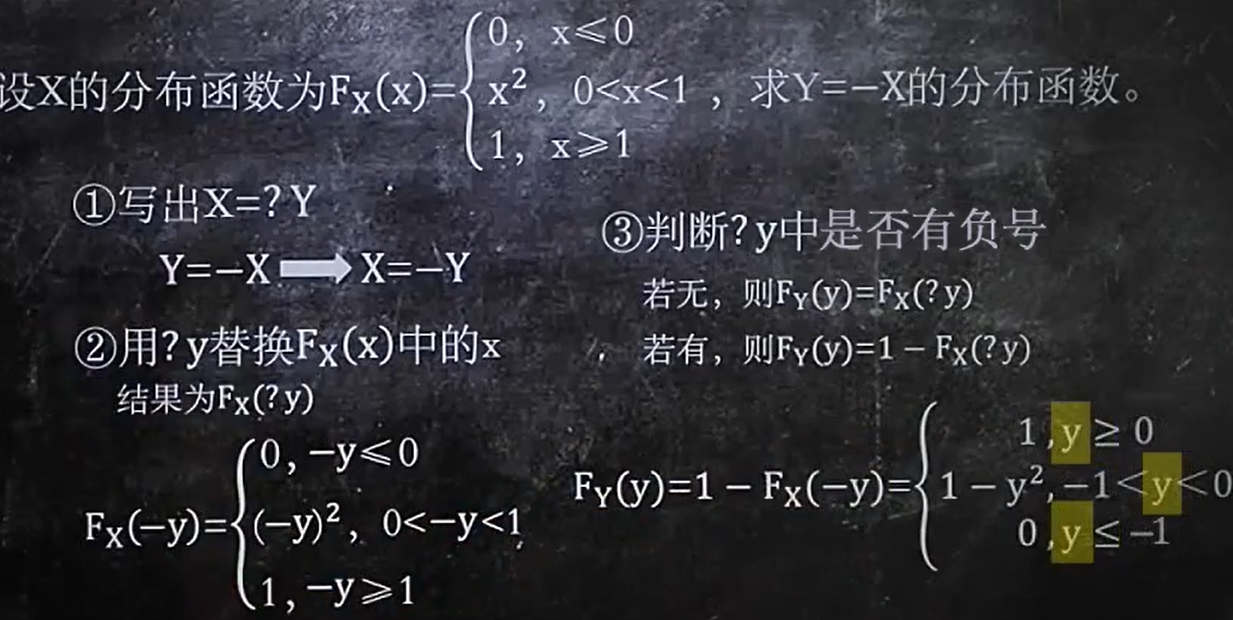
3、已知fx(X),求fy(Y)
同样的套路
- 写出x等于什么什么y
- 用什么y替换fx(X)中的x,结果为fx(?y)
- 令fy = (?y)' * fx(?y)
- 判断?y中是否有负号,如果有就是求得的答案的相反数

第四章(六大分布)
首先给出各种分布的分布律、概率密度、E(x)、D(x)
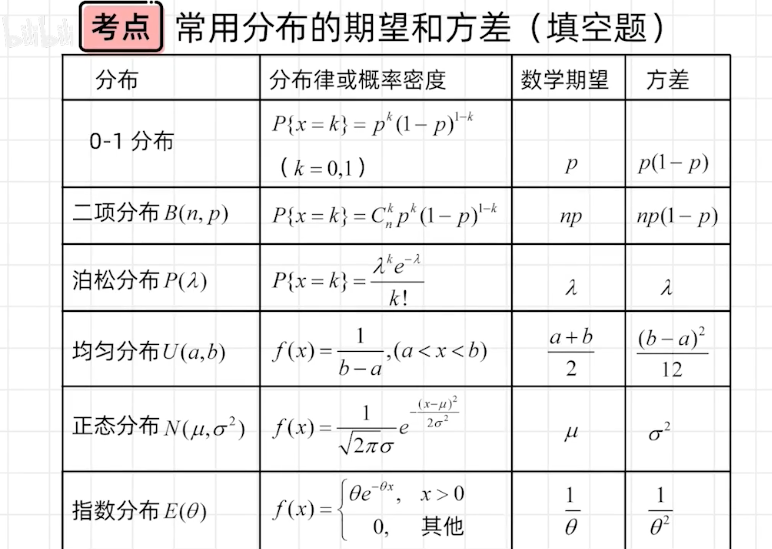
1、符合均匀分布,求概率

2、符合泊松分布,求概率
lambda是参数,x是某某次数

如果是这样的,千万不要用1-P(X=6)这种,要一个一个算!

3、符合二项分布,求概率
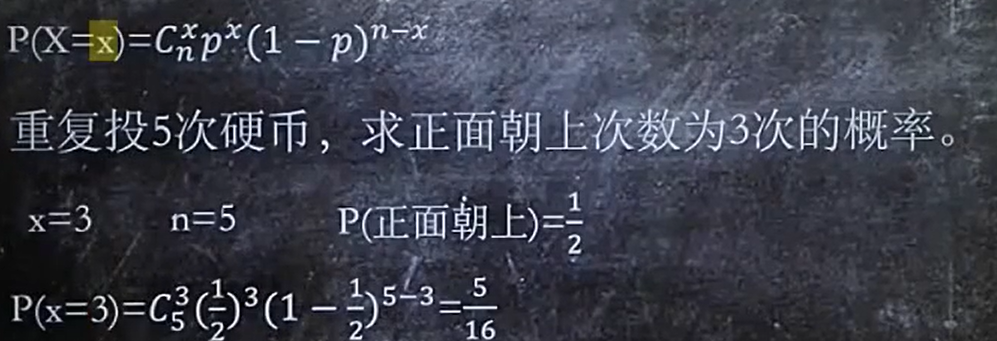
4、符合指数分布,求概率
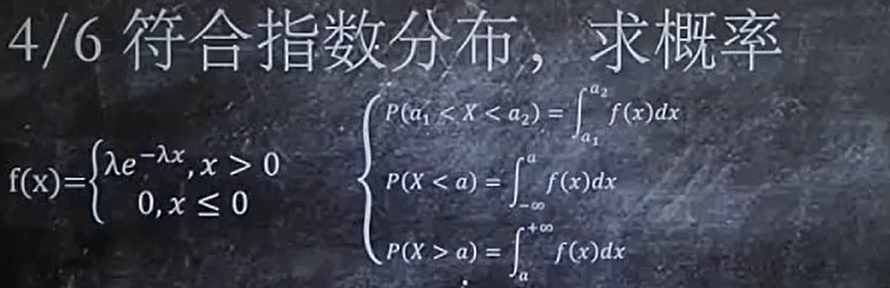

5、符合正态分布,求概率
正态分布还是很重要的,后面也会经常用到标准化公式(x-u/o)
一定要记住fai(0) = 0.5
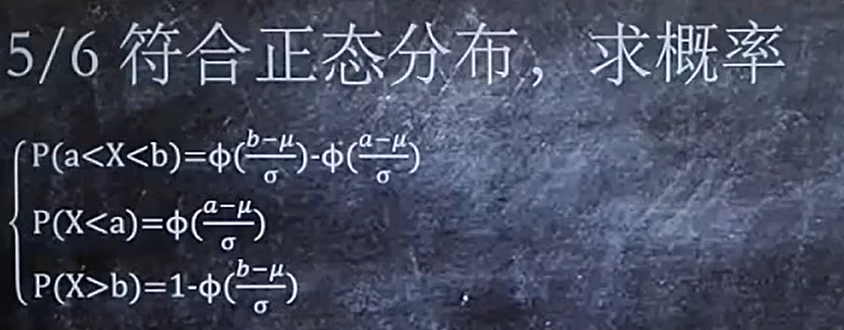
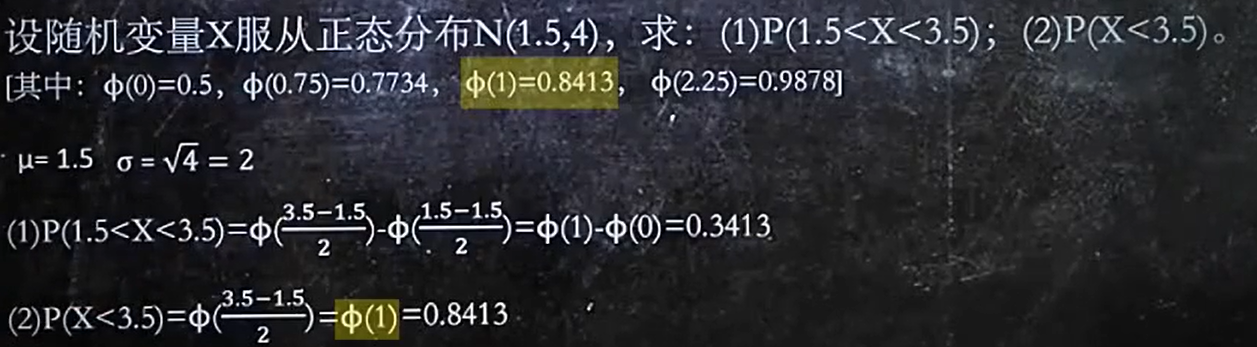
6、正态分布图像
1.面积表示概率,整个正态分布图像的总面积为1
2.图像关于u对称
3.o越小,图像越陡

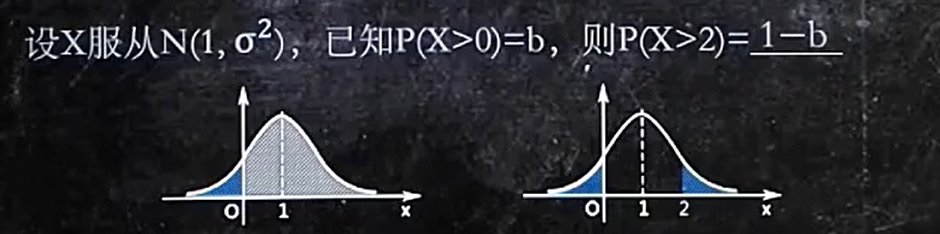
看陡峭
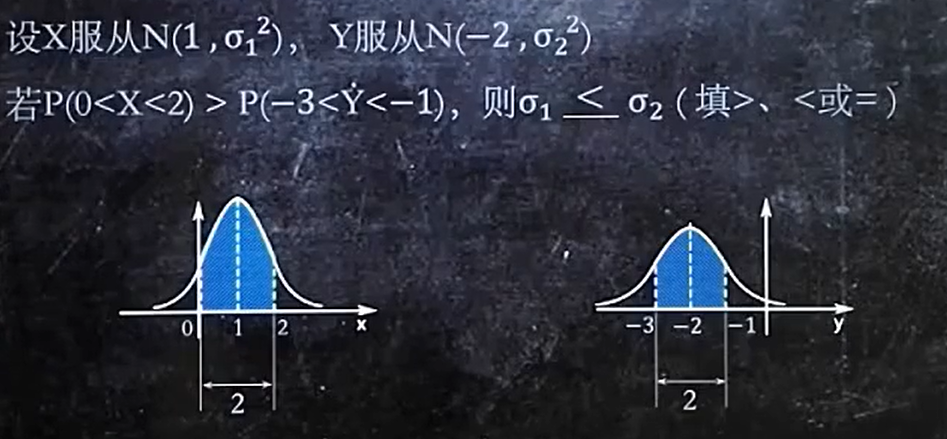
7、各种分布的符号

第五章(二维随机变量)
1、已知二维离散型分布律,求???
离散型的就看表就好咯
例如:

查表:
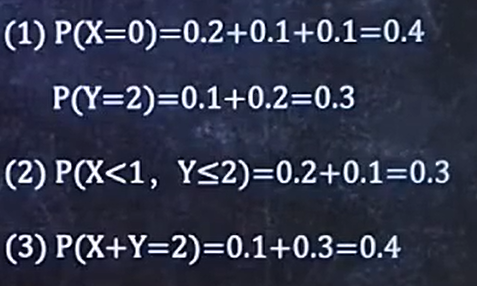
作表:
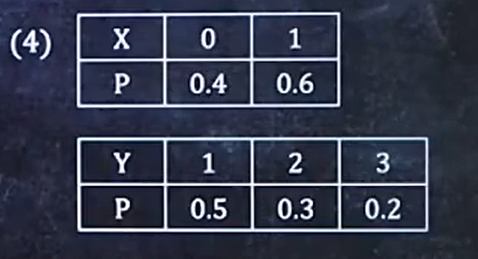
穷举:
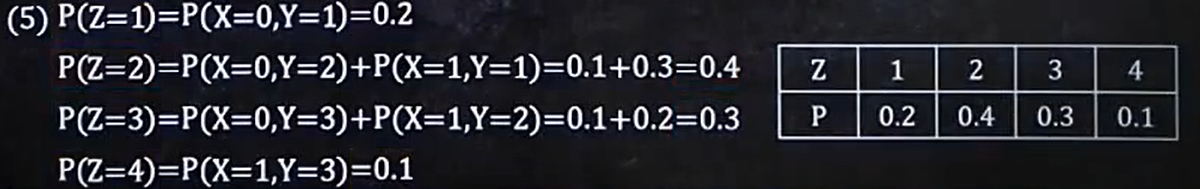
2、已知二位离散型分布律,判断独立性
如果满足p(xy) = p(x) * p(y),那么相互独立
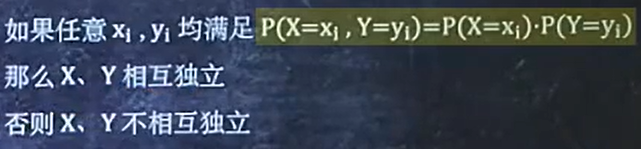
例1:
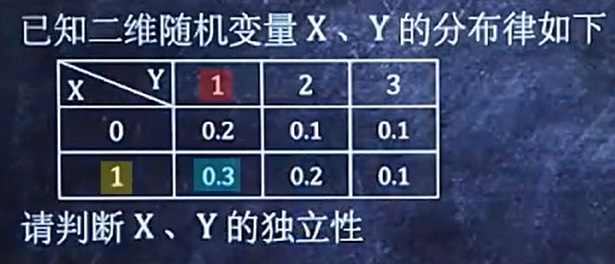
我们只需要验证每一个p(xy) = p(x) * p(y),就可以验证独立性
例2:
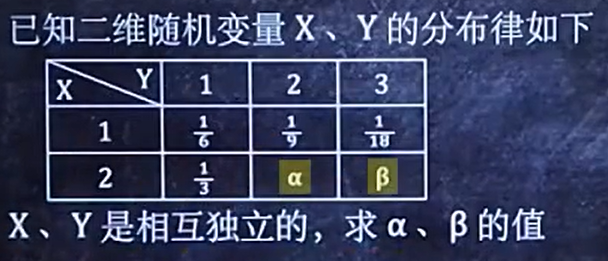
因为独立,所以
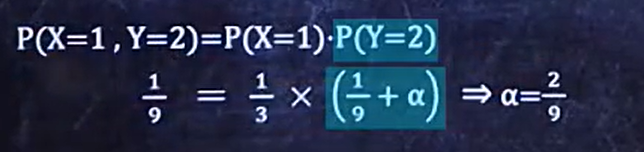
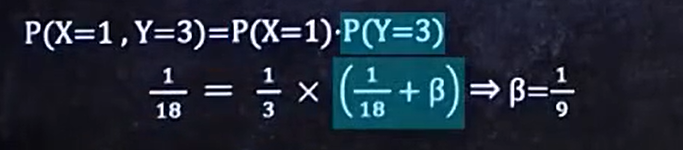
因为所有的概率是1,所有我们求出一个a就可得到另一个b的概率
3、已知F(x,y)求f(x,y)
F(x,y)是联合分布函数
f(x,y)是联合概率密度
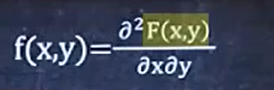
例如:
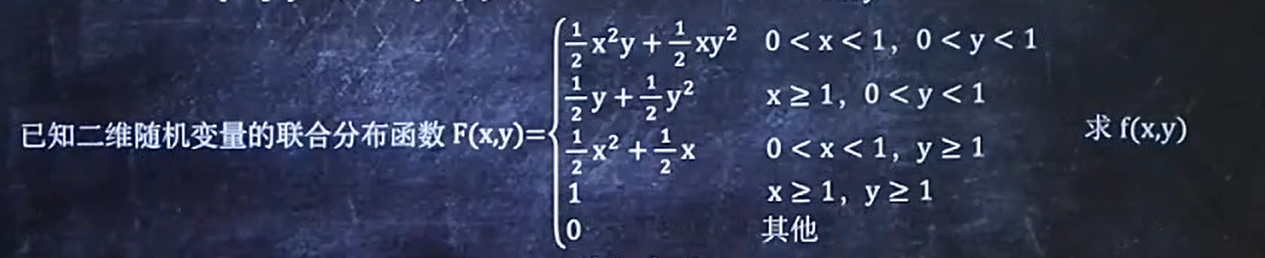

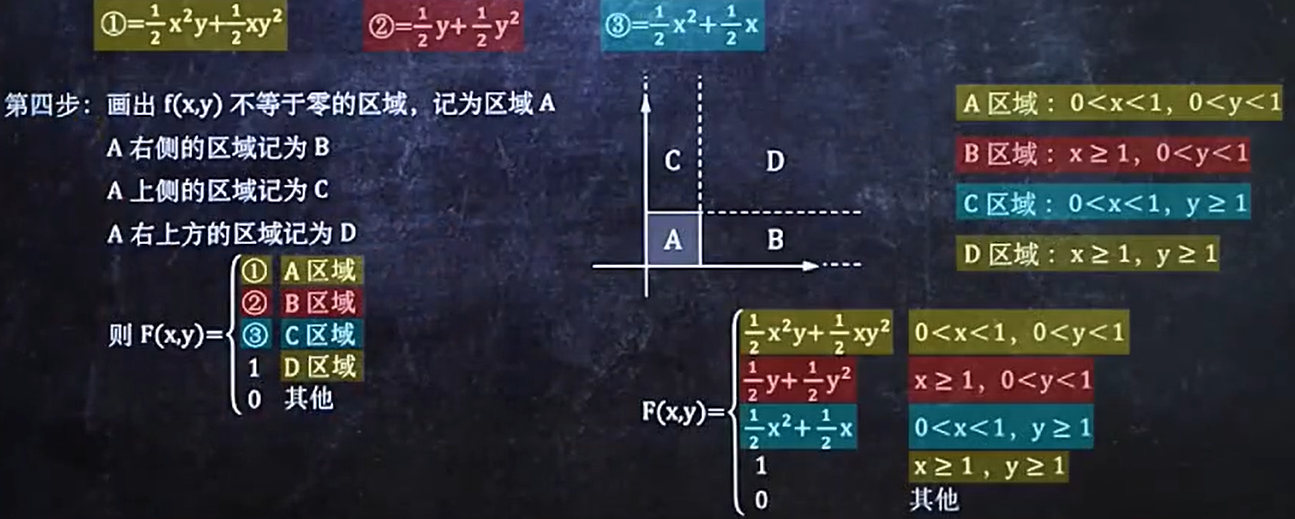
已知f(x,y)求F(x,y)
- 找出f(x,y)不等于0时x的范围和y的范围
- 计算结果
- 带入计算
- 区域
例题1:



例题2:
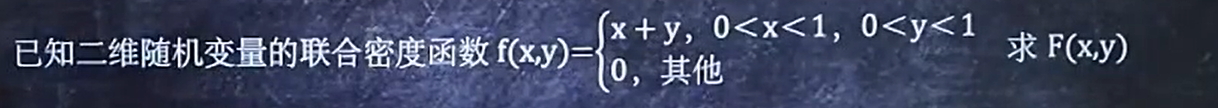

5、已知F(x,y)求P
记住公式然后带入
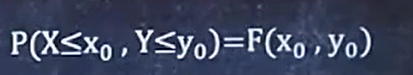
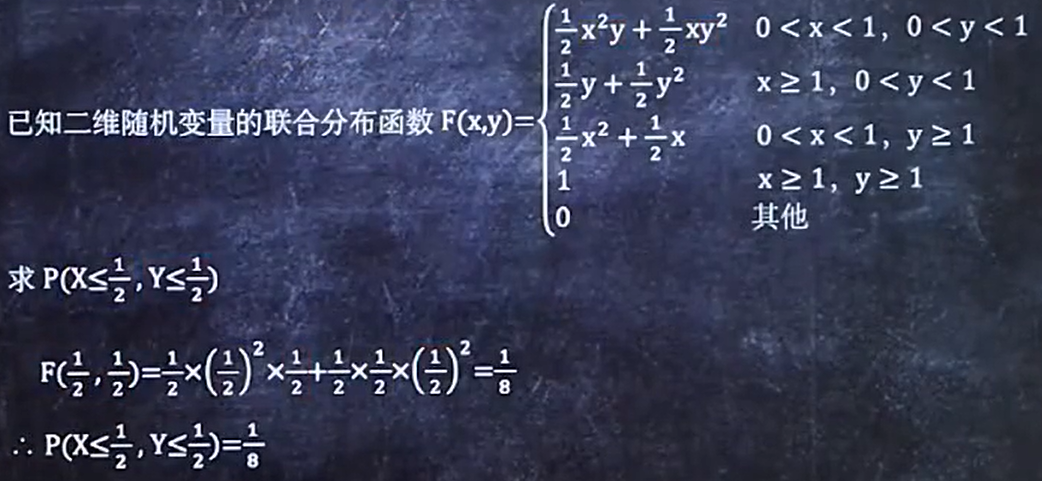
加一点变形:
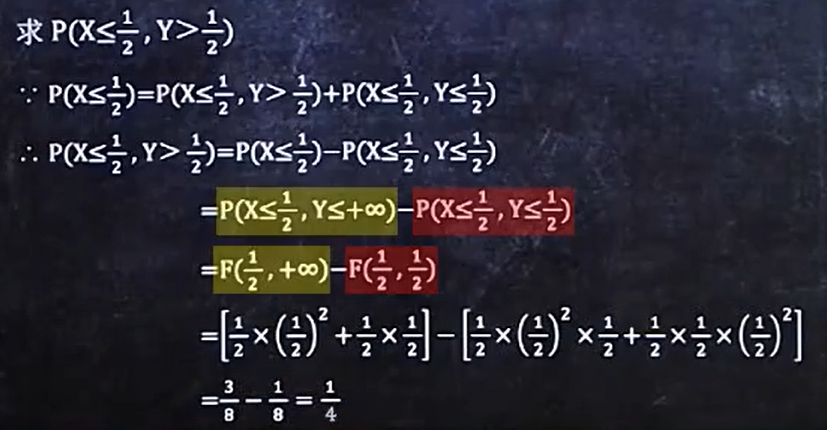
6、已知f(x,y)求P
注意解题步骤,求范围再带入求更细的范围,再带入二重积分中
例题1:
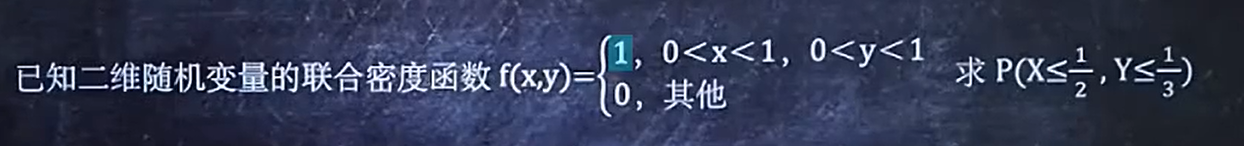

难一点的例题2:
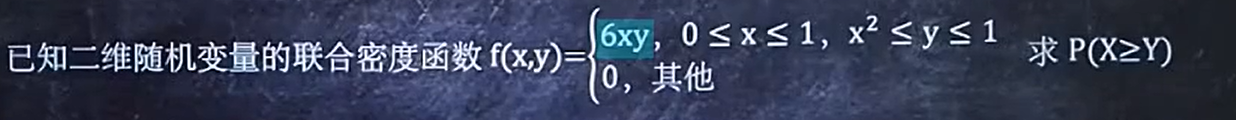

7、求F(x,y)或f(x,y)中含有的未知数
记住下面的式子

8、求均匀分布的f(x,y)与P
记住式子:

例如:
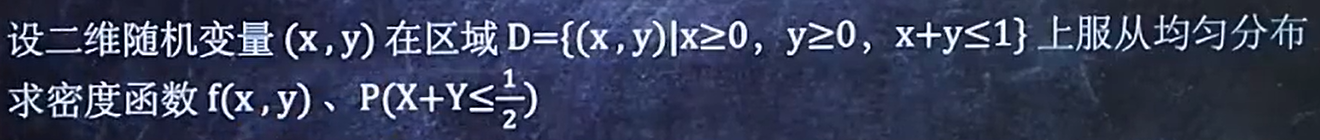
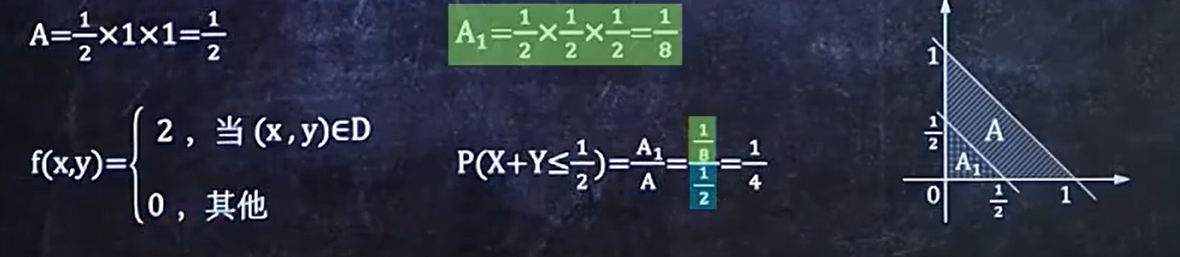
第六章(边缘分布)
1、求边缘分布函数
记住如下公式:

例如:
带入公式即可求解

2、求边缘密度函数
F(X,Y)是边缘分布函数
fx(X),fy(Y)是边缘概率密度
有公式:
fx(X) = f(x,y)dy在y的无穷界限上的积分
fy(Y) = f(x,y)dx在x的无穷界限上的积分
例题:
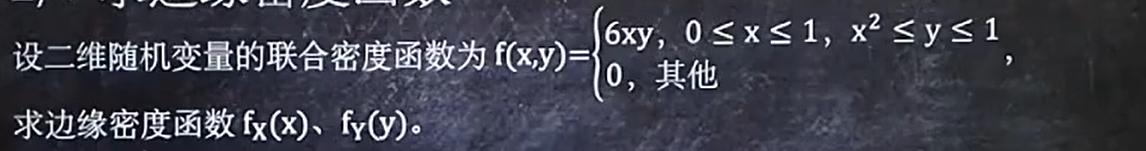

3、判断连续型二维变量的独立性
F(x,y) = Fx(X) * Fy(Y)那么X、Y互相独立
f(x,y) = fx(X) * fy(Y)那么X、Y互相独立
这种题目带入验证就可以了
先求出 fx(X) 和 fy(Y)带入计算验证就OK了
如何求出 fx(X) 和 fy(Y)在上一个题型说了
例题:

4、一直f(x,y),Z=X+Y,求fz(Z)
记住关键公式:(卷积公式)

例题:
记得分类讨论就好啦

5、已知f(x,y),Z=x/y,求fz(Z)
记住公式:
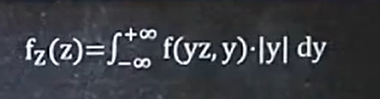
例题:
解法和上题一致,就是公式使用不同

6、已知f(x,y),且X,Y相互独立,Z=max(X,Y),求Fz(Z)
记住一个公式:Fz(Z) = Fx(Z)*Fy(Z)

7、已知f(x,y),且X,Y相互独立,Z=min(X,Y),求Fz(Z)
就是和上面的题目的公式不一样:Fz(Z)=1-[1-Fx(Z)]*[1-Fy(Z)]

第七章(期望与方差)
1、求离散型的期望E(x)
简单题,高中方法求期望就好了
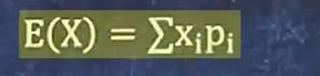
例题

2、求连续型的期望E(x)
连续型的期望公式:E(x) = xf(x)dx在无穷上求积分
公式如下:
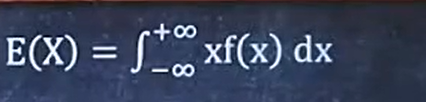
例题:

3、已知Y=g(x),求E(Y)
公式如下:
其实也很好理解,之前的连续性E(x)=xf(x)dx求积分,那么带入下面的Y=g(x)=x,也就是得到xf(x)dx

离散型的例题:

连续型的例题:

4、求方差D(x)
记住两个公式(主要是第二个D(x)=E(x2)-[E(x)2]

例题1(离散型):

例题2(连续型):
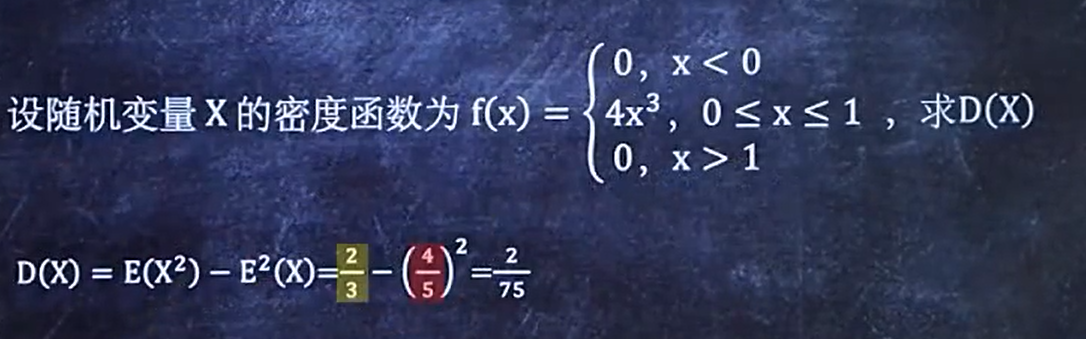
5、根据E(x)、D(x)的性质进行复杂运算
看表:

例题:
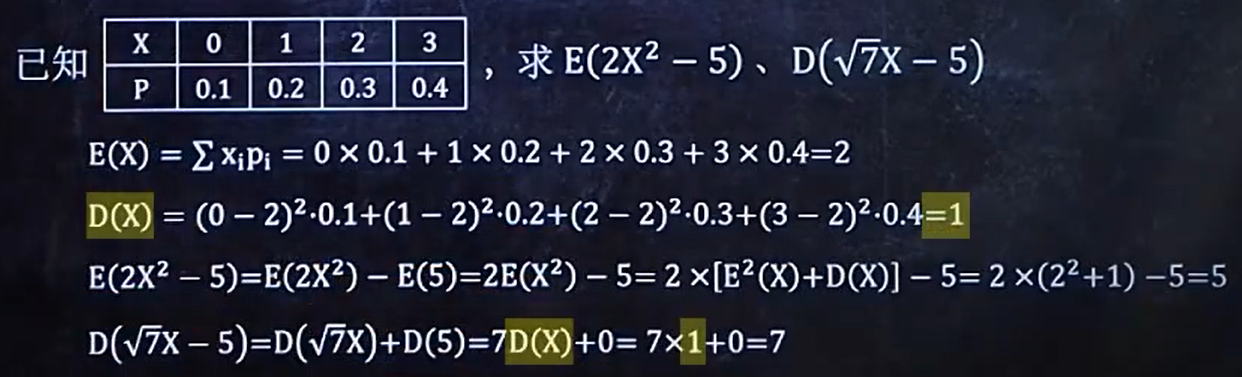
6、E(x)、D(x)与各种分布的综合题
各种分布的公式:

例题1:(二项分布)
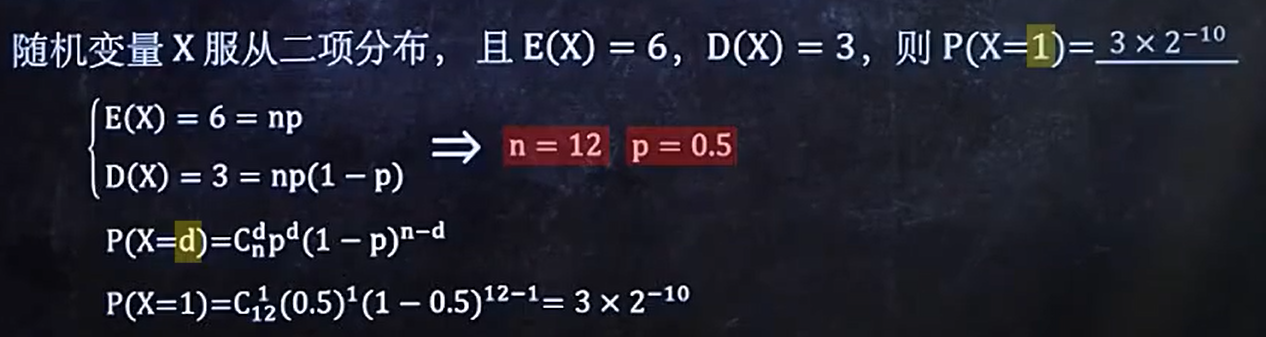
例题2:(泊松分布)

第八章(协方差)
1、Cov、ρxy、D相关类题目
开背:
 例题1:
例题1:
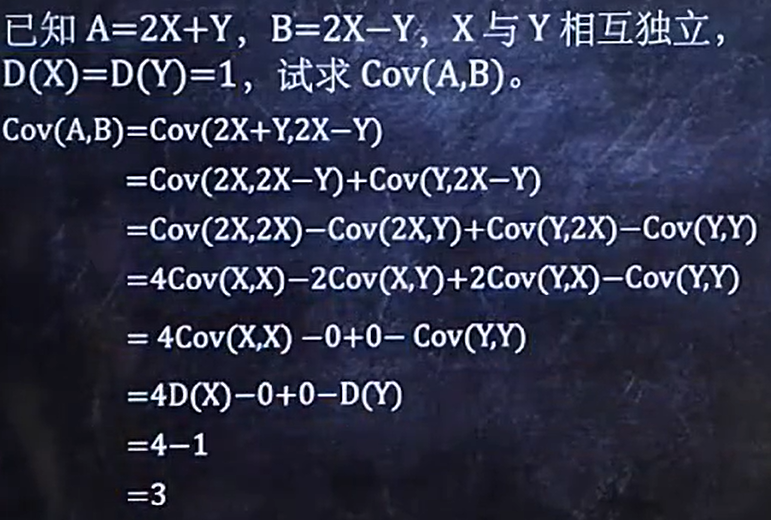
例题2:

2、利用切比雪夫不等式求概率
有公式:

例题:

3、多项独立同分布,求总和怎样的概率
还是看公式:
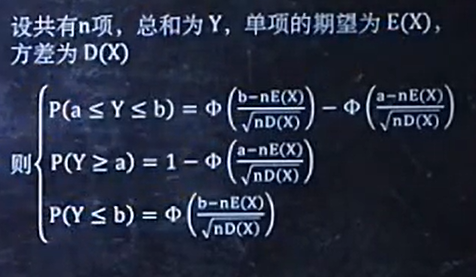
例题1:

例题2:

第九章(三大分布)
1、常用统计量
①样本均值 
②样本k阶矩
③样本方差
④样本标准差
⑤样本k阶中心矩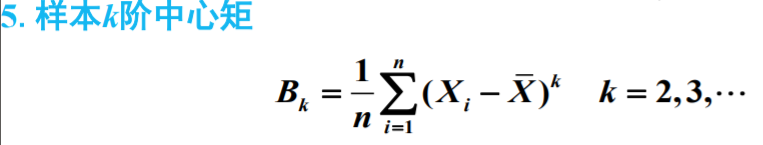
注意B2和S2的区别(一个是1/n-1,一个是1/n)
2、三大分布
分别是χ2分布(卡方分布)、t分布、F分布
χ2分布有可加性、Ex=n、Dx=2n



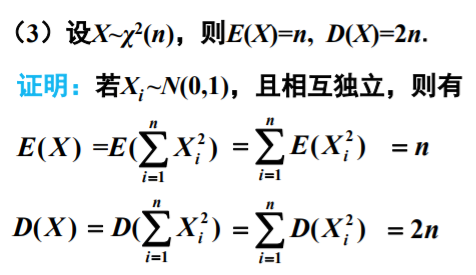
t分布的Ex=0、Dx=n/(n-2)



F分布,上下都是卡方分布

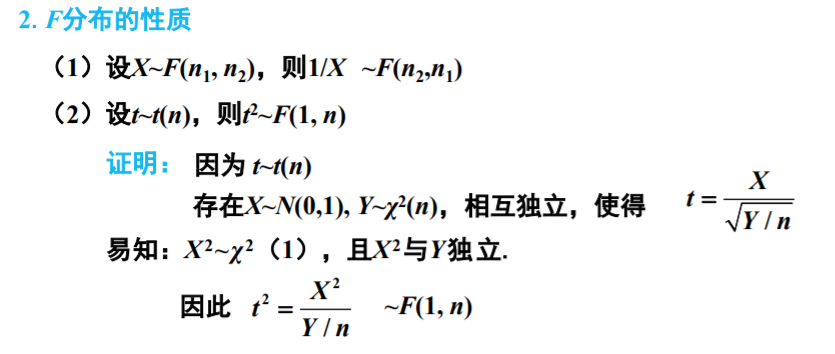
第一章(矩估计)
1、求某一未知参数的矩估计
步骤如下:

例题1:

例题2:

-
先用公式求出E(x)
-
然后写出未知数等于多少E(x)的形式
-
写出实际的E(x)
-
最后将实际的E(x)带入到未知数方程中,得出答案
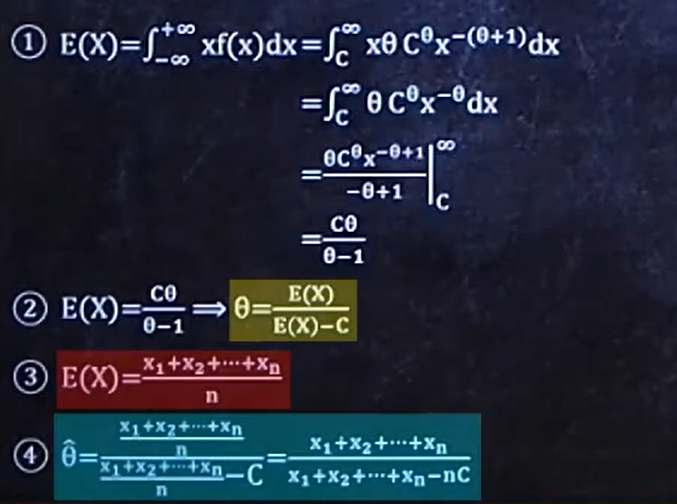
2、求两个未知参数的矩估计
步骤如下:

例题1:

书上例题
- 算出E(x)和E(x2)
- 写出未知数等于?E(x)+?E(x2)
- 根据给出的样本求出实际的E(x)和E(x2)
- 求出未知数就是矩估计

第二章(最大似然估计)
1、求出某离散型参数的最大似然估计量
步骤如下:

例题1:

-
写出每个x的分布律
-
对每个分布取ln
-
对ln的结果求导
-
令求导的结果为0,求出未知数
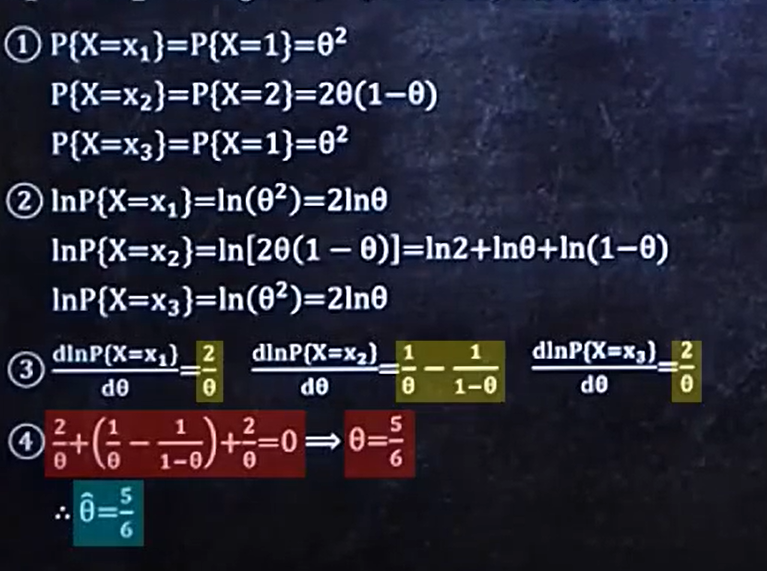
2、求出某连续型参数的最大似然估计量
步骤如下:

和上一类型差不多,这里第一步先求每个fx就可以了
例题1:

- 求出fx1、fx2、fx3...fxn
- 对每个fx求ln
- 对ln结果求导
- 多个求导结果相加要等于0,求出未知数

第三章(区间估计)
区间估计
看表!考点有标准化等

单个正态总体参数的区间估计(老师的ppt)

两个正态总体参数的区间估计(老师的ppt)

一定要记住前面的三个分布!!!
此外,书上p175页也有上图的公式
背完上面的公式我们来看例题~
例题1:

首先看求什么的置信区间,是求μ的,那么就是正态分布标准化公式的那套
其次置信水平为0.95那么1-α=0.95,α=0.05,所以α/2=0.025
并且没有σ,所以我们需要用s来代替σ
因为(n-1)s2/σ2满足t分布,所以有如下的置信区间
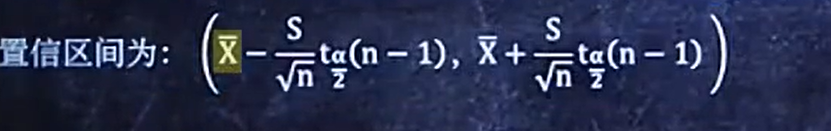
将算出的各种值带入求解:

例题2:

首先分析求哪个的置信区间,可以看到求σ的,那么就是套卡方分布那套
置信水平0.95,1-α=0.95,α=0.025
又因为μ没给,就用(n-1)s2/σ2~卡方(n-1),得到σ2的置信区间:
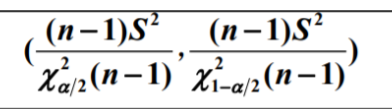
带入求就好了
注意!!!上图的置信区间是σ2的,我们要求的是σ的,需要根号一下!
答案:

还有可能考μ1-μ2的类型,背表!!!!
第四章(假设检验)
假设检验
和上一章内容有关,假设检验这里就学了一共6个公式
第一种类型——Z检验法:
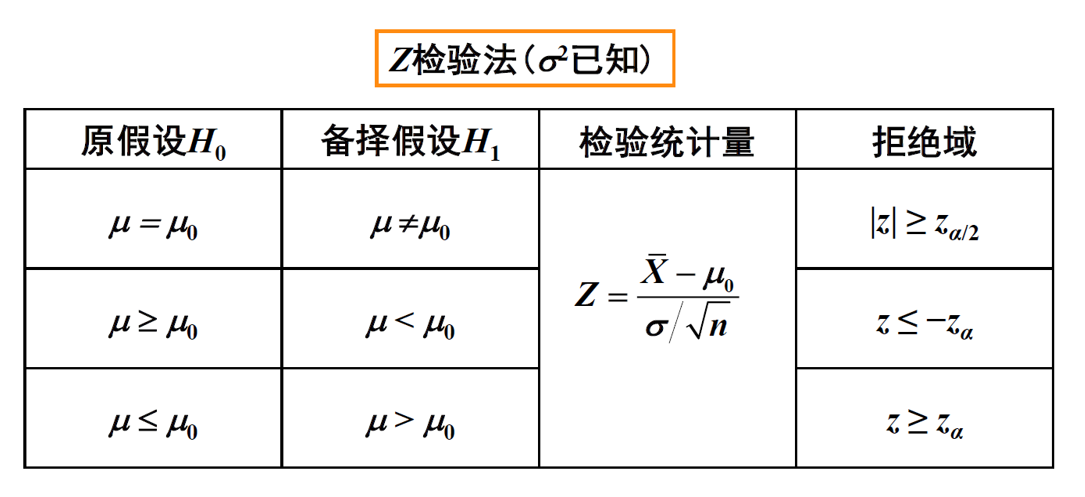
第二种类型——T检验法:
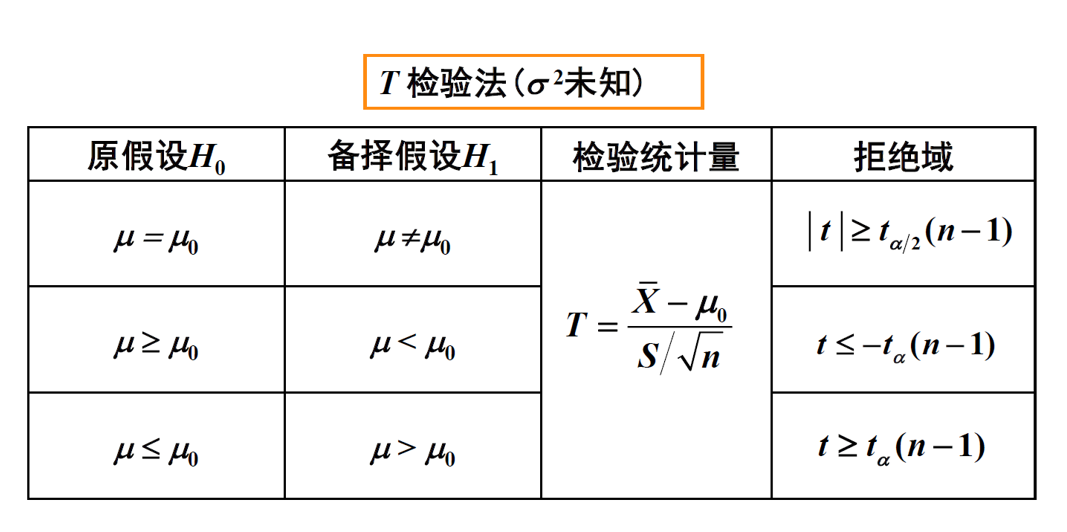
需要注意的是,我们的原假设尽量是向良好的结果假设。
另外就是拒绝域问题,我们求出来的值在拒绝域之内,就是被拒绝了,就是不符合我们的原假设。在拒绝域之外就是良好的,符合我们的原假设。
例题就看书上的p215页的三道题目就好了